Atomic Radiation: Measuring Techniques
July 1969 Electronics World

July 1969 Electronics World   Table of Contents  Wax nostalgic about and learn from the history of early electronics. See articles from Electronics World, published May 1959 - December 1971. All copyrights hereby acknowledged.

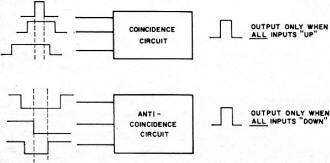
This is Part 3 of a 3-part series of articles on atomic radiation that appeared in Electronic World magazine in 1969. It deals with measurement techniques and equipment. Shippingport Atomic Power Station, the first full scale nuclear power plant in the United Sates, went operational in 1957. It marked the dawn of a new era of electric power generation that was filled with grandiose predictions of limitless, non-polluting, dirt cheap power. Everything was going to be powered by electricity - air heating and cooling, lighting, automobiles, refrigeration, cooking, water heating. Atomic power was going to be a figurative and almost literal beating of swords into ploughshares as the destructive energy of nuclear weapons was put to use in powering the world. People were still getting used to the concept of being a nuclear citizen and wanted to be educated on the subject. Many articles such as this one appeared in every sort of magazine from Electronics World to The Saturday Evening Post.

Author Joseph Wujek published a 3-part article in Electronics World in 1969 to address the issues. Here is Part 1 - Types & Relationships, Part 2 - Detection Methods, and Part 3 - Measuring Techniques.

Part 3. An examination of the basic circuits that are used in spectroscopy to measure accurately the amount of radiation.

By Joseph H. Wujek, Jr.

Before examining some of the circuits and systems used in radiation measurement, we should state the design goal of an ideal radiation measurement system.

Ideally, a radiation measuring system should detect the presence of radiation, identify the types of radioactive particles, and measure the flux level (number of particles per unit area in a given time period). The last function - sorting out the number of particles of a particular energy over a given time interval, is called "obtaining a spectrum of the radiation, or "performing pulse-height analysis." Of course, there may be additional design goals. We may require that the system perform calculations, such as averaging particle counts over a given time period and to display and/or print out these results. We may also require

the system to sound an audible and/or visual alarm when thee radiation level exceeds some predetermined level. Too, we may require a very high resolution system, so that small energy differences between particles can be realized. There may also be a requirement to measure very low energy particles existing in the presence of high "natural" or "background" radiation, thus demanding a low-noise system with good background rejection. And, finally, the system may require a high degree of measurement precision, that is, a system which remains stable over a long time period regardless of use, variations in ambient temperature, or power-supply voltages. Clearly, every measurement system does not require all of these refinements. But most systems encountered in nuclear spectroscopy are designed with these considerations in mind.

Language of Nuclear Instrumentation

Unfortunately, many engineers in the nuclear instrumentation field use jargon or some words which are completely foreign to other areas of electronics. A good example is found in the expression "full-width at half-maximum." This rather verbose statement is simply a measure of the sharpness of a spectral line and hence is not very different from the "Q" used elsewhere in electronics. Other examples of this unique and sometimes cumbersome language is the scalar (flip-flop or bistable multivibrator) and the coincidence gate (and gate). Because workers in the industry persist in using this terminology, we offer a short glossary in Table 1 to aid the newcomer to the field. More formal and extensive definitions may be found in the "Standards of the Institute of Electrical and Electronics Engineers for Nuclear Science."

Radiation Detector Circuits

All radiation detectors used in spectroscopy require some kind of amplifier. Fig.  1 is a simple amplifier used to provide "charge" amplification. In Part:2 ("Atomic Radiation: Detection Methods"), we showed why the capacitance of some detectors is dependent upon certain bias conditions and why it is advantageous to measure the charge deposited by an incident particle rather than to measure a voltage change.

If the circuit in Fig. 1 is treated as an operational amplifier, certain simplifying assumptions can be made. They are: the amplifier has high open-loop input impedance and high open-loop voltage gain. Thus. e_o = Q/C_f. This same circuit is used to perform the integration operation in analog signal processing. Again, if we assume the feedback capacitor C_f is a stable element, the output voltage is proportional to the charge generated by the detector. In most commercially available systems, temperature stabilities of better than 0.01% per degree C and voltage gains of 10 to 100 are common.

Resolution and threshold is detector limited, not electronically limited. In fact, circuit development has kept pace with detectors. Preamplifiers using FET input stages and solid-state detectors can be operated at very low temperatures, thus reducing system noise. (Most noise sources are strongly temperature dependent.) Bipolar transistors used in earlier systems exhibited considerable gain degradation at low temperature but FET devices do not, thus the FET system also improves over-all performance.

Systems have been operated at temperatures near liquid nitrogen with good results. The boiling point of liquid nitrogen is about 320° below zero F. At these temperatures there is relatively little thermal energy in the atoms within the crystal lattices, hence, little noise.

In addition, amplifiers used in radiation detecting instruments must be capable of fast recovery. Often, input signals several hundred times the input pulse amplitude occur, sufficient to saturate the output. These pulses severely overload the output. But, a recovery time of several microseconds is indicative of the state-of-the-art.

Pulse-shaping is an important consideration in establishing over-all system performance. Linearity, time-resolution, noise, overload recovery, and over-all precision are affected by the pulse-shaping network.

Perhaps the most commonly employed pulse-shaper is the simple RC-differentiator, often used in pulse work as well as linear circuits. Fig. 2 shows the RC pulse-shaper along with two of the more common schemes for shaping which employ delay lines. The various trade-off's, which determine which scheme is "best" for a given application, will not be discussed here, except to note that the choice is often dictated by system restraints.

Discriminators find widespread use in nuclear systems. Within the context of the present discussion, a discriminator is a circuit which changes its output state when prescribed conditions are fulfilled at the input. An integral discriminator is a circuit which changes state and remains in that state, as long as the input is above (or below) a given voltage. A differential discriminator changes output state as long as the input remains between two given voltage levels. This voltage difference between these levels is commonly called the "window." In the more descriptive language of digital circuits, the integral and differential discriminators are, respectively, termed single-ended and double-ended differential voltage comparators.

The discriminator finds use in pulse-height analysis of the output of detector amplifiers. An array of these circuits can be used to route an output pulse to a particular counting channel, as shown in Fig. 3. Scalars, or other means, are used to count the number of pulses of each particular energy band (energy is proportional to pulse height), thus generating a spectrum (Fig. 4). Commercial pulse-height analyzers are available which show the spectrum on a CRT face, print out the number of counts in a given energy channel (band), and otherwise gather data from a pulse-height source. Systems of 1024 channels and more are available "off-the-shelf."

Coincidence and anticoincidence circuits (Fig. 5) form another basic building block in nuclear detection systems. A coincidence circuit yields an output, if and only if, two or more inputs signals are simultaneously present. The familiar and gate is an example of a coincidence circuit. The anticoincidence circuit provides an output whenever signals are not present at the same instant. This function is also readily implemented with familiar digital circuits. Sophisticated coincidence and anticoincidence systems have been built which can resolve events occurring fractions of a nanosecond apart. Since many atomic reactions occur in sub-nanosecond times, these systems are extremely useful to the nuclear physicist.

The count-rate meter (CRM), which may or may not have a meter associated with it, is another useful circuit. The CRM, by the nature of its design, is at best a 1% instrument in terms of precision. In many applications, however, 1% is more than adequate.

The CRM is primarily an integrator and produces a voltage (or current) proportional to the rate at which pulses are applied at its input. In performing this function, the CRM is not unlike the pulse demodulator or the amplitude detector in an AM radio. Fig.  6 shows the principles involved in CRM circuitry.

So-called logarithmic count-rate meters have been built in a variety of configurations. One type employs a logarithmic ("log") amplifier as a stage. Others feature "scale change" circuits which automatically sense and change scale when the count rate goes outside the limits of the CRM scale in use at the time interval in question. Dynamic ranges of 10⁵ and more can be fashioned in this way.

The availability and low cost of digital integrated circuits and associated readouts have tended to displace the CRM. However, narrow bandwidth requirements, small size, low power requirements, and circuit simplicity considerations tend to offset the digital circuit advantages in favor of the CRM. Remote sensing, as in space experiments, may impose severe restrictions on the number of available data lines, again favoring the CRM. In field instruments and certain special applications, the count-rate meter remains an important design.

One other system is worth noting because of its widespread use in nuclear instrumentation. The analog-to-digital converter (ADC), long used in computers, is used extensively in counting systems. Many varieties of ADC's exist, but most have in common the gating of a precision frequency. Fig. 7 shows the elements of a simple ADC. An integral discriminator compares the amplitude of the incoming pulse (stretched for a time period compatible with the conversion time) with a ramp voltage of precisely con­trolled length and amplitude. When the ramp begins, pulses of known frequency are gated into a scalar chain. When the ramp voltage reaches the voltage of the pulse, the pulses are gated off by the action of the discriminator (comparator). The number of pulses stored in the scalar chain is thus proportional to the amplitude of the signal. The ADC is then reset and awaits the next incoming signal for a repeat of the cycle.

In practice, ADC's have been built with clock rates of 100 MHz and more, and conversion times of fractions of a microsecond. The precision of the conversion is proportional to the number of digital bits (flip-flops used) and hence, in the scheme just outlined, the time of conversion. Thus, if we had six scalars and a 10-MHz clock, conversion could take as long as 6.3 μs. This is found by taking 2⁶ - 1 = 63, the bit storage and multiplying by the clock rate of 100 ns. Other schemes, some rather elaborate, improve upon this basic time conversion and precision limitation.

In addition, the somewhat unique (unique to nuclear work) applications of the circuits already described, nuclear instrumentation systems make use of a variety of hardware common to the electronic art. Core memories, X-Y plotters, CRT outputs, digital printers, to name just a few, are often an integral part of a nuclear counting system. Direct interfacing with computers is becoming commonplace, enabling the scientist to escape much of the routine work of experimentation and data reduction. Improvements in detectors, especially in low-noise detectors, enable the experimenter to perform measurements which were beyond the state-of-the-art only months earlier. As with so much in modern science and technology, electronics holds the key to new discoveries.

Posted February 15, 2018