|
<Previous
Next>
Resistor Cube Equivalent Resistance
 See
additional info below. See
additional info below.
Probably the most responded-to article I have ever written is the "The Resistor
Cube Equivalent Resistance Conundrum," aka Kirt's Cogitations™ #256. Having
equal resistances in all branches usually makes things easier. An alternate method
of solution,
posted here, was provided by RF Cafe visitor Les Carpenter.
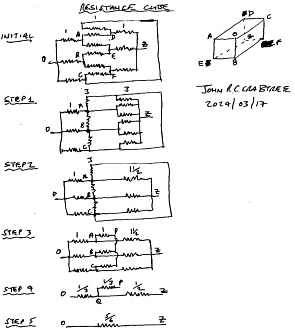
A couple days ago, another approach to the solution was submitted by Mr. John
Crabtree. As with the others, his work demonstrates an intuitive way of looking
at the circuit that simplifies a solution. Whereas my method invoked knowledge of
currents into and out of nodes, then dividing that current into a voltage applied
across two opposing corners, John combines parallel and series resistances until
a final single equivalent resistance emerges.
I like his old school pencil and paper presentation rather than a computer drawing.
It reminds me of the days when teachers wrote on a transparency on an overhead projector
(while students frantically tried to copy it down and comprehend what is
being discussed at the same time).
This goes to show how there is usually more than one way to solve a complex problem,
and no version necessarily earns the
Occam's
Razor title.
April 3, 2024 Update for Polyhedral Resistive
Structures:
Not being satisfied with merely providing the solution for the resistor cube,
Mr. Carpenter followed up with an application of the "Equivalent Resistors
of Polyhedral Resistive Structures" method shown to the right. Note, again,
everything hand-written. He states:
Equivalent Resistors of Polyhedral Resistive Structures

John also provided a hyperlink to a paper on the ResearchGate
website entitled "Equivalent
Resistors of Polyhedral Resistive Structures," in which author F. J. van Steenwijk
(University of Groningen,
the Netherlands), provides a method for solving any regular geometric solid shape
with equal resistances along each edge, being connected at the corners.
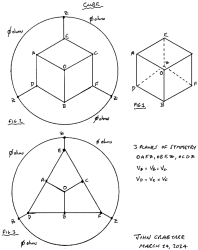
Nodal symmetry for resistor
cube (6 faces, 8 vertices, 12 edges).
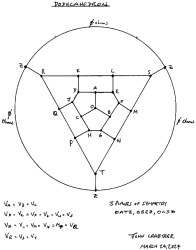
Nodal symmetry for resistor
regular dodecahedron
(12 faces, 20 vertices, 30 edges).
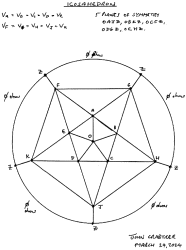
Nodal symmetry for resistor
regular icosahedron
(20 faces, 12 vertices, 30 edges).
The paper by F. J. van Steenwijk is beautiful. Having a current of I / (H - 1)
leaving the remaining terminals is a wonderful insight.
Before you post anything, I should tell the other part of the story.
This puzzle has been around for over a century. For instance it appeared in Brooks,
E.E. and A. W. Poyser, Electricity and Magnetism: A Manual for Advanced Classes,
Longmans, Green, 1914. I found this reference [for a
Resistor Tesseract].
It was also in the 1912 edition of the same book. I hav[n't] seen any earlier references
to it.
And yet there seem to be very few efforts to draw the circuit as a planar network
which shows the three planar axes of symmetry through the cube.
I set out to do this, and considered what the cube would look like if it were
drawn on a great circle map with the input node at the centre and the output on
the other side of the sphere. That got me to Fig. 2 on the cube page in the attached
file. I then straightened some of the lines which got me to Fig 3. The three planes
of symmetry in the cube are now very apparent, which makes the points of equal voltage
apparent. This makes the parallel resistor solution very straightforward.
Fig. 3 also makes it very straightforward to seen the current distribution, and
derive a solution by summing voltages.
I suggest to you that Fig. 3 makes the problem very much easier, if not trivial.
I then wondered if others had tried to draw the network in the same way. I did
find Fig. 2 in: i) "Symmetry in Science:
an introduction to the general theory", Joe Rosen, Springer-Verlag, 1995, pp
110-115. ii) "A Symmetry Primer
for Scientists", Joe Rosen, John Wiley, 1983, pp 124-129 iii) "Symmetry
discovered : concepts and applications in nature and science", Joe Rosen, Cambridge
University Press, 1975, pp 114-117. You can read all of these books at http://www.archive.org.
This is as much as I have found.
I have also drawn diagrams for the same problem for the icosahedron and the dodecahedron.
Again the planes of symmetry and hence the equipotential points are readily apparent.
In closing, in my diagrams the points of equal voltage lie on concentric circles.
These circles are equivalent to the equipotential planes in Fig. 1 of van Steenwijk's
paper. I see things better in two dimensions!
73 John KC0G
I found the hyperlinks to the Archive.org books John references, and also linked
to the Wikipedia pages for the geometric solids.
Posted March 28, 2024
|
 "
"



