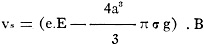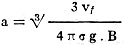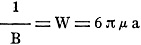An Interesting Experiment in Weighing the Electron
and What It May Mean
September 1932 Radio News

September 1932 Radio News [Table of Contents] Wax nostalgic about and learn from the history of early electronics. See articles from Radio & Television News, published 1919-1959. All copyrights hereby acknowledged.

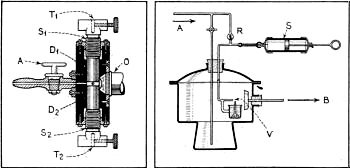
"We might say almost, that all modern scientific investigation in the basic sciences, and a good deal of all practical developments, are connected in some way or other with the electron." So writes Dr. Irving J. Sax in this 1932 issue of Radio News magazine regarding the incentive for determining as precisely as possible the mass and electrical charge of an electron. The Bohr atomic model had just been introduced two decades earlier, so the entire concept of particle physics was still in its infancy. As with most areas of physics, experiments are conducted with particular biases and expectations such that often the results are manipulated as needed to conform to preconceptions. Look no further than the complex retrograde motion planetary models devised and perfected by early astronomers who believed the universe revolved around the Earth. It wasn't until a heliocentric model was accepted (following the exile and execution of many "heretics") that orbital systems became simplified and readily explainable. The same, to some extent, has been true of subatomic particle physics, except digging deeper into the true nature of the beast has continually revealed greater and greater complexity. Each time a new "fundamental" particle is discovered through empirical testing, an new, more basic element is theorized and must be explored; to wit, the Higgs Boson (aka "God" particle). Indeed, even the planetary-like Bohr model of the atom was proven incorrect by the advent of quantum mechanics and the ensuing electron orbital cloud model based on probability distributions (in 1932, the year of this article in fact, by Mullikan). It was a mere five years prior to the publishing of this article that Heisenberg had formulated his "Uncertainty Principle" that limited the precision with which a particle's speed and mass could be determined. None of this subtracts from the importance of each step along the way, and in fact, augments the need to continue investigating the fundamental aspects of nature's building blocks. For the particle physics historian, this article will prove to be a treasure trove of information.

An Interesting Experiment in Weighing the Electron and What It May Mean

By Dr. Irving J. Saxl

In all our modern electronic technique, including radio technique, television, acoustics and in all other basic sciences connected with electricity we are making use and apply constantly the electronic theory and its fundamental unit, the electron.

We have considered the electron to be the smallest entity of matter, having one single, definite electric charge and include it in our formula, whether we are now building radio tubes, X-ray tubes, motor-generators or whether we are making intricate electrical measurements. We might say almost, that all modern scientific investigation in the basic sciences, and a good deal of all practical developments, are connected in some way or other with the electron.

We are living in a century of electrification. New electrical machines, appliances and instruments are still being given too humanity at high speed - and all of them go back, in their last root, to our knowledge of the electrical phenomena and its basis: the electron.

But what do we actually know about this tiniest entity of the universe? It is the commonest thing in the cosmos, there is no atom of matter in which there is not at least one electron, and yet, what is it in reality, this most important, minutest quantity of the microcosmos?

The theory that a material body is composed of tiny "building-stones," which cannot be divided, is not new. The Greek philosopher, Democritos, had written of it already and even in the Hindu philosophy, first signs of this idea appear in a general way.

Today there are a number of units which we cannot subdivide chemically. We call them elements. From Faradays experiments on electrolysis it was found what amounts of a certain material can be electrolytically deposited within a certain time. It is now possible to determine the number of molecules of which the deposited substances are composed by using the laws which have been given us by Loschmidt, making it possible to determine, mathematically, the number of the molecules contained in each cubic centimeter. Using this number, called "Loschmidt's Number," and using the data taken from Faradays' laws it has been possible to determine the average charge of a single ion. It was found to be in the order of 10^-10 electrostatic units.

Around the year 1900, Townsend, J. J. Thomson and A. H. Wilson carried on further determinations of average values which also gave an electric charge of about 10^-10 for the monovalent ion.

Of course, as far as electronics technique is concerned, the single electron does not seem to be today of industrial importance. What is important is the effect of a vast number of electrically-charged bodies which, after all, make important for practical use only the average value. For going deeper into the matter, however, it is important to know more about the individual happenings within a physically defined body.

If we have a carload of potatoes, can we say the size of the potato is this and that? Is it not probable that, if we observe a large-enough number we will find small ones and large ones ... and that the small ones might be almost any size smaller than the larger ones? Can we take the "average potato" and say: this is THE size of the potato?

Can we, therefore, state positively that there is no smaller charge in the world? We have subdivided the molecules and we have subdivided the atoms which, as the name expresses, "cannot be subdivided any further." Is the electron, on the knowledge of which we base so much of our present-day physical knowledge, is it really the last bit of matter? Or is it just one step farther into the unknown depths of the universe?

It was Dr. Felix Ehrenhaft, Professor of Physics at the University of Vienna who wrote in 1909: "Smallest entities of electricity are, as far as can be predicted, to be expected upon particles of smallest capacity" and, "These particles, however, have to be large enough to make them just individually perceptible optically, as it is necessary to investigate each one separately." *

For determining the size, the weight of these particles, the relation between their electrical charge and constituting matter, the important entity e/m, , we naturally cannot apply a chemists balance. Even the finest balances for Pregls micro-analysis are crude in comparison with the values which have to be determined for this purpose. Other ways have to be found for bringing about this determination.

However, a condenser balance has been developed making possible the incredible exact weighing of body-particles smaller than the tiniest dust particles which we see dancing in an intensive ray of sunlight if we look normally upon this projecting ray.

The test particles which are to be investigated are brought into the field of an electric condenser. They are strongly illuminated from the sides and are viewed through a microscope. By putting electric charges across the condenser plates it is then possible to move these particles up and down between the plates by electrostatic attraction and repulsion.

From these movements of the particles in the condenser, the exact time of which is determined, it is possible to calculate both the weight and the charge of the body as described in greater detail at the end of this article.

Acting upon his idea, Ehrenhaft tried to take into consideration for his experiments, particles of well-defined form and chemical characteristics. He therefore worked with small globes of gold, platinum, silver, mercury, etc. The spherical form of his particles he was able to show by microphotographs in white light. For fully resolving still smaller bodies, the author has helped perfect for him the application of ultra-violet-microphotography, following early designs of Prof. A. Koehler.† A microscope using these principles has been manufactured by Zeiss and used in this country for the optical analysis of alloys.

For making visible these very small particles, Ehrenhaft constructed a special tiny condenser. It consists principally of two round plates of brass or iron of about 1/4 inch in diameter and spaced about 1 millimeter apart. These condenser plates form the walls of a very small air chamber (see Figure 2 which shows a schematical cross-section through the condenser that was used in all the tests on the particles).

The two cylindrical pieces, D₁ and D₂, of which the condenser is made, are screwed in from the upper and from the lower ends. By means of the screws, S₁ and S₂, it is possible to correct their distance precisely. 0 is the front lense of the microscopic objective through which the particle is viewed. The illumination takes place, normally, upon the cross-section of the condenser and upon the axis of the observing microscope, as shown in the close-up of the front of Ehrenhaft's apparatus in Figure 3. The observation is made between the condenser plates D which are embodied in a housing of Bakelite. T₁ and T₂ are the terminals into which the contacts of the electric conductors are screwed securely. The gas, which is chemically and physically purified and in which the test particles are suspended, is brought into the viewing condenser by means of the stopcock A.

The Set-up Employed

Figure 3 shows the front view of the apparatus at the eyepiece of which one observer is to sit. 1 and 2 are the illuminating arcs. These are high-intensity, self-regulating, direct-current arc lights burning with about 30 amperes. It is necessary to use 2 separate sources of illumination as during the long duration of the observations one pair of carbons may burn out. A second pair of carbons is therefore always ready for use in the other projector so that it can be put into use immediately and make possible a continuous observation. In addition, these two light sources put against each other in an angle of 180 degrees are necessary also for another reason:

Most particles brought into the path of this highly intensive light react in a specific way upon the irradiation. Dependent whether they are light-positive or light-negative they move to the light source or run away from the source of light. (This effect, called Photophoresis and probably in definite relation to the photo-electric principles involved in photocells, was discovered by Ehrenhaft.)

By using two separate lighting units, diametrically opposed to each other, it is possible, simply by illuminating from the opposite direction, to push a particle back into the center of the observation field. This change in illumination is done with the aid of the electro-magnetic shutters, 3 and 4, which are operated from a double-pole switch, 5.

The particles, which have been formed in the desiccator, 6, are brought through glass tubing into the condenser. The microscope, 7, is the device through which the particles in the condenser are observed. The actual illumination takes place from the left and the right. For eliminating the effect of infrared heat rays, the light, after coming from the projectors and the shutters, passes through two filters containing a solution in the horizontal cylinders 8 and 9. The light beam is concentrated into the condenser field with the aid of two microscopic objectives, 21 and 22, so that an extremely intensive "dark-field" illumination is secured. For avoiding any indirect heat-radiation, the two projectors are placed behind the asbestos walls 10 and 11.

Time Recording Important

The amount of voltage applied across the condenser plates can be regulated by the rheostats 12 and 13. The switch, 14, makes it possible to change, instantaneously, the polarity between the two plates. With a foot switch, 17, this voltage is put onto the condenser plates.

The telegraph keys, 15 and 16, at the left lower side of the picture, operate automatic stop-watches electromagnetically. These watches can be read down to one-fiftieth of a second. They record the time of ascent and descent of a particle within the condenser, the path of which is viewed upon a grid in the observing microscope 7. This path is not a straight line, up and down, but moving in different curves. The particle dances about following the Brownian movement; a twinkling spot upon a dark background in the observing microscope.

The exhaust gauges, 18, consist of a series of small capillary tubes through which the exhaust gas has to pass and by means of which it is possible to regulate the speed of the exhaust procedure. On the manometer, 19, the air pressure in the electric condenser can be read (through a little telescope which is on the assistants desk). 20 is a McLeod, an instrument with which pressure (of a fraction of one millimeter) can be read down to microns.

The observer looks into the eyepiece of the microscope so as not to loose the path of his particle. He is kept very busily engaged in regulating the voltages which change sometimes, especially if an accidental radioactive material has been in the neighborhood of the condenser or other effects have taken place as to liberate electric charges, for instance, by irradiation with ultraviolet light. The observer has furthermore to start and stop the procedure, to regulate the exhaust, to work the light switches so that he cannot afford the time to make actual recordings. Mechanical recording has therefore been applied for these intricate investigations, under the control of an assistant.

Figure 4 shows the assistant's table. It is placed behind the observer's seat, as at the assistant's table lights are necessary. Meanwhile the entire room is kept dark so that the observations will not be effected by any outside light. In Figure 4, 1 and 2 are the electro-magnetically-controlled stop-watches.

The actual voltage put across the condenser plates and regulated by a shunt, is read on the precision voltmeter 3. The air pressure in the condenser is read over a system of reflecting mirrors with the small telescope 4.

Producing the Particles

The test particles were produced by three different methods: No. 1. The first method was to build an electric arc between two pieces of metal. This arc smelts off minute drops of the metal to be used as particles. They evaporate from the electrodes and coagulate in the colder atmosphere which surrounds the electrodes in the form of balls of the dimension 10^-4 to 10^-5 cm. No.2. The second method employs bodies which can be evaporated and these are brought into a small container of glass or quartz and heated with a small flame (Mercury, Sulphur, Selenium, etc.) to liberate a steam which condenses in the form of small balls. No. 3. Figure 5 shows the third method of producing balls of a heavy fluid as e.g. Barium-Mercury-Iodine, Mercury, etc. These small balls will always be geometrical spheres of great accuracy where the capillary powers are larger than the forces which bring about the "drop" form. A vaporizer V in which specially purified gases are sucked through the opening with the aid of a syringe-like pump, S, distributes small particles of the fluid in which it is immersed.

The specific weight of this fluid is known and therefore also the specific weight of the particles. These fall very slowly, due to their sub-microscopic size. They are contained in the gas current and are transported together, with it, through the funnel, B, into the condenser field.

There the particle is irradiated strongly from the side, as stated above, and it is seen in the microscope as a luminant point upon a dark field. It is possible to read the distance through which the particle falls freely in the air-condenser chamber, upon a grating which is inserted into the eyepiece. If the particle carries an electrical charge and if the plates of the condenser are charged electrically, it is possible to move the particle upward by electrostatic power! It is also possible to measure here by its speed!

The particle is allowed to fall again after switching off the electrical field so that it moves downward under the influence of gravitation. This procedure is repeated long enough so as to receive satisfactory averages of the ascent and descent of each particle tested.

If a sphere falls in a space filled with gas, its speed of fall does not get larger into the infinite. The friction of the sphere in the air works against gravitation and after a certain time, the friction gets so large that the ball moves with a constant speed. With a submicroscopic sphere as used in Ehrenhaft's experiments, this constancy is reached after a very short time.

Investigations have shown that the velocity of such a particle is proportionate, within certain limits, to the power acting upon it. Stating v for velocity and P for power, we get the equation:

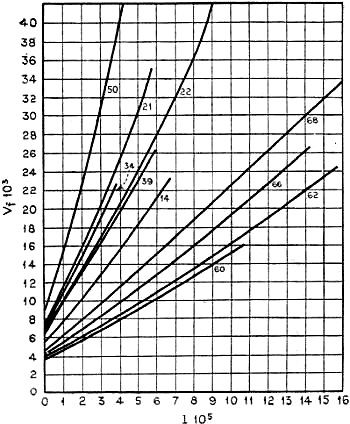
(1)    v = P.B.

where B is a factor of proportion. Its physical meaning is the velocity under the influence of the power which is unity. B may be called the mobility of the particle.

For a free-falling body of spherical form we have, therefore, the equation:

(2)   

where V_f is the velocity of the fall, a is the radius, σ is the density and g is the gravitational acceleration.

If the particle is pulled upward again under the influence of the electrical forces put unto the condenser and has the velocity v_s, then we can say:

(3)   

where e is the electrical charge of the particle and E is the field intensity in the small condenser.

From equation (2) can be computed the radius of the particle:

(4)   

It is necessary to know, from other sources, the value of B, of the mobility of the particle. This known, it is possible to determine the electric charge of the particle, by simply inserting the value for a, from the equation (4), and the value for E (which we can read directly on the voltmeter) in the equation (3).

The mobility B has, therefore, to be found in some other way if we want to determine the radius and the electric charge of our particle. Stokes, the English mathematician, calculated for the resistance W - which is reciprocal to the value of the mobility B - which is impressed upon a sphere during its motion through a fluid:

(5)   

It is assumed hereby that the fluid sticks continuously to the surface of the sphere.

For a sphere, however, which moves in a gas instead of a fluid and with reasonable speed, too, it may not be correct to suppose that the medium will stick to the surface. Aeromechanics and hydro mechanics have shown that this case practically never happens. The so-called "laminar"-movement takes place only under theoretical conditions, assuming an almost infinitely small movement of an inelastic body in a fluid of small hydraulic mobility. Practically in all cases eddies and whirls appear which disturb markedly Stokes' law. Experience teaches against the theory that the gas glides along the surface of the exposed body and, in addition, the formation of whirls takes place for gases which are so dense that the average free-mean-path of their molecules is small against the radius of the sphere (that means sufficiently smaller than 10^-5 cm.).

It has been necessary, therefore, to correct Stokes' law. Following the calculations of Stokes-Cunningham, this formula reads:

(6)   

Where l is the average free-mean-path of the gaseous molecules and A is a constant (which gives a value for the gliding and is supposed, following the theoretical calculations, to be near unity).

Will experiments at different gas pressures especially in compressed gases, be able to solve this problem?

Investigations at different pressures under one atmosphere have been already made. Figure 6 shows a diagram of measurements which have been taken for each individual particle at different pressures by Dr. Max Reiss. From these experiments which have been made between 1 atmosphere down to about 50 mm. pressure, it seems that some particles have a smaller density than the molecular material. On the other hand, particles have been found, which indicate much smaller values for the supposedly standard electric charge of an electron! It has apparently been possible to measure single electrical charges as low as 1.10^-10 electrostatic units, that is less than one-fourth of the values found by other investigators.

For giving an idea about the incredible small forces with which we have to deal and which we have to control experimentally in these intricate investigations, it may be mentioned that the forces which act upon the particle are of the dimensions of 10^-10 dyne. This corresponds to an attraction with which two containers of about one quart of water each act upon each other over a distance of about 2 miles!

If the particles with which he operated were small enough, Ehrenhaft's measurements on individual particles showed values for the separate electronic charge which went far below the quantum charge which is required by the theory. From other methods the value of the electronic charge was determined to be about 4,77.10^-10 electrostatic units. Dr. Robert A. Millikan in Pasadena who described the condenser method at about the same time as Ehrenhaft††, and who was awarded the Nobel prize found this larger charge.

In addition to having found smaller charges than the elementary quantum Ehrenhaft states that it is not directly possible to consider the electric charges he found, as simple multiples of the elementary charge. These conditions of being able to build simple multiples, quanta, would be a necessary requirement, if one of the cornerstones of modern physics should be a true natural law: the quantum theory of Max Planck which has proven so valuable a tool for many investigations.

According to Ehrenhaft, it would be necessary to determine the value of the unit of negative electricity much lower than 47.10^-10 electrostatic units ... provided that there is existing any atom of electricity at all.

In practice we continue, today to use the electron as such in our calculations and our engineering. But will we, under these circumstances, consider the electron as a truly existing standard entity ... in the scientific world of tomorrow?

* Wiener Akadem. Anz. number 7 March fourth, 1909.

† Ehrenhaft & Wasser, Philosophical Magazine. Vol. 11. 1926.

†† R. A. Millikan: Physical Review XXIX, p. 260, December, 1909, F. Ehrenhaft: Anzeiger d. Wiener Akademie d. Wissenschaften March fourth, 1909.

Posted January 27, 2022
(updated from original post on 4/15/2014)