Design Tips for Rewinding Your Own Transformers, October 1944 Radio News

Not many people rewind transformers these days, but then even in 1955 when this "Design Tips for Rewinding Your Own Transformers" article appeared in Radio News magazine not many were rewinding transformers. Plenty of radio repair servicemen did, though, because replacements were expensive and getting replacements for other than common transformers could take a long time. There was no searching for one on the Internet and having it delivered in a couple days. Since many - if not most, by necessity - electronics repair shops kept subscriptions to available trade magazines, publishing an article like this provided a great service. Author James Dolan provides all the necessary information for either designing your own transformer from scratch or for modifying an existing transformer to meet your specific requirements. Many shops kept a topically arranged index card file listing the magazine name, issue number, and article title for quick reference.

Many servicemen must, of necessity, rewind small, defective radio transformers in view of present-day shortages.

Save those old transformer cores. Many of them can be used for self-designed units for special jobs.

Lack of priority, special experimental work, urgency, a desire to design and construct your own transformer, any of these reasons may lead you to attempt the design and the construction of your own transformers. This article is intended to assist the prospective transformer builder who has been saving a stock of cores with the intention of making something out of them someday. To the constructor of transformers is opened the possibility of constructing transformers for his own special uses, to his own specifications, and in whatever electrical size he wishes.

As the experimenter generally plans to use cores which he has on hand, whether they be from some old discarded broadcast job, or something he overloaded once too often, or the parts of a pole transformer gained by a wise alliance with some local power company, this article will attempt to show how those cores can be put to good use.

The first consideration is the size of the cores on hand, both physical and electrical. Get a little notebook and then measure all of the cores on hand, putting this information into your notebook. Our first consideration of design will be the wattage of the transformer we are planning to make. Accordingly, it would be wise to list our transformer core stock in regards to the wattages which they will carry. Also listed, should be the thickness of the core, the cross-sectional area of the center leg if the core is of the shell type, and the cross-sectional area of one leg if it is of the core type. The area and length and width dimensions of the window in the core into which the completed coils must fit should also be recorded. It is quite disconcerting to wind up a coil and then find that the window of the core is too small to receive the completed winding. It is well to allow 10% to 40% extra space allowance in making coil size computations unless you happen to have some sort of winding machine, such as a good lathe with proper change gears, on hand with which to wind your coils, as otherwise you are not going to attain the winding spaces shown in the common wire tables which give so many turns per square inch. Do not try to squeeze the winding into the least possible space; allow for your errors and the departure from perfection that you are sure to make.

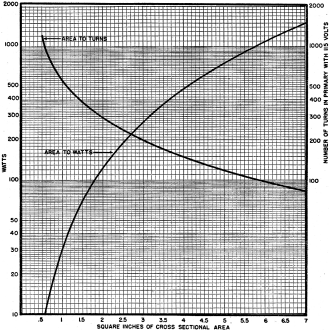
The only tool required for the first part of our work is a good ruler; measure the outside dimensions of the cores, their length and width, the window area, and the thickness of the core. Compute the cross-sectional area from these figures. Remember to clamp the core up tightly when measuring the thickness, or an error will result in your computation.

The wattage that the core will handle is found by reference to the graph given for this purpose. This graph has the wattage ratings on the left-hand vertical column and the cross-sectional area is at the base of the graph. A curve on the graph is marked "Area to Watts." Find the cross-sectional area . on the base scale and follow a vertical line erected at the point representing the area up to the "Area to Watts" curve. Where this vertical line meets the curve draw a horizontal line to the left to the wattage column. This will indicate the wattage-handling capabilities of the core.

Fig. 1 - Follow these curves carefully when designing your own radio transformers to obtain maximum efficiency and operating performance.

The next consideration is the use that is proposed for the cores on hand. If a requirement for a transformer comes up, have you a core that can be used for the purpose? That is the first question that must be answered; find the wattage. Wattage is equal to the product of voltage and amperage, or:

Thus, we must multiply the voltage by the amperage of each secondary and add these together to find what wattage is required. Let us design and construct a transformer which will deliver 5 volts at 3 amperes with a center tap; 6.3 volts at 4 amperes with a center tap; and have a high-voltage winding of 450-0-450 volts and which will deliver 200 milliamperes of current. The transformer will operate on 115-volts, 60-cycle current. Applying our formula (1) we have, 5 x 3 is 15; 6.3 x 4 is 25.2; and 450 x 200 milliamperes or 0.2 ampere, is 90. These products represent the wattages of the individual secondaries. Add them and the total secondary wattage is the result, in this case, 130 watts. The primary wattage is found by adding to this figure the losses in the core and windings. Usually these losses are about 10% of the rating of the transformer. Therefore, if we divide the secondary wattage by 0.9 we will find the primary wattage; thus:

in which W_p represents primary wattage and W_s represents the secondary wattage.

If this is done, the primary wattage for the transformer is 144 watts. Let us call this 150 watts in order to secure an easy working value.

We can stop right here and consult our previously made chart in our notebook showing the cores on hand and the data on them. Have we a core on hand that will handle 150 watts? Perhaps a sheet of silicon steel must be purchased from a local steel dealer and cut up to make a core type transformer. Perhaps we have a 200-watt core on hand from which we can subtract a few laminations to use it for a 150-watt application.

Now, due to the power factor of the transformer we cannot divide this wattage value by 115 volts in order to find the current, but must take this power factor into account. As the power factor is generally about 90% we can find primary current by multiplying the primary voltage by 0.9 and dividing the primary wattage by this product.

If 115 volts is used for the primary voltage, this product (E_p x 0.9) becomes 103.5; if the primary voltage is 110 volts, the product becomes 99. If we wish to secure an easy figuring value, we may call this product 100, which would represent a primary voltage of a little over 110 volts. If we use the factor of 100 in our proposed transformer design which has a primary wattage of 150 watts, we find that our primary current will be 1.50 amperes.

The next step in the design is the calculation of the turns in the windings. The graph indicates the primary turns for a 115-volt primary using a core flux density of 75,000 lines per square inch. As all types of steel will be in the cores that we shall use, it is necessary to pick out a value which is high enough for good operation and still not so high as to cause excessive core losses with the poorer grades of steel. This table is made by assuming the primary voltage as being 115 volts and the frequency 60 cycles per second. It is easy to use the graph; having the core area (cross-sectional) on the base line, erect a vertical line from the base at the point representing the core cross-sectional area to the line marked "Area to Turns." At the point where this vertical intercepts the curve so marked, extend a horizontal line to the right-hand side of the graph where the turns in the primary circuit will be indicated.

Going back to the proposed transformer that we are building, it is noted again that the core has to carry 150 watts. Consulting our graph we find that the cross-sectional area required for this power of 150 watts is 2.2 square inches. The primary will have 270 turns of wire as shown by the "Area to Turns" curve.

As we have the primary turns from the graph, we can find the secondary turns for each winding by application of the formula stating that the ratio of primary voltage to primary turns is directly proportional to the ratio of secondary voltage to secondary turns. Mathematically this is: E_p/N_p = E_s/N_s

This formula is made more usable by transposing it into a more workable form in which the factors are changed to indicate turns per volt rather than a proportional ratio problem. Thus, as turns per volt is the number of turns divided by the voltage, one term of our new formula should be in this form:

The new formula now states that the secondary turns is equal to the primary voltage divided by the primary turns and this result is to be multiplied by the secondary voltage. In our proposed transformer we have found our primary turns to be 270; substituting this value and inserting the primary voltage into our equation (5) we have:

Now, by substituting the various secondary voltages in place of E_s in our formula we can easily find our secondary turns. Our proposed transformer has three secondaries, 5 volts, 6.3 volts, and 900 volts, all center-tapped. Using the above formula we find that the 5-volt winding requires 12 turns; the 6.3-volt winding requires 14.8 or 15 turns; and the 900-volt winding requires 2115 turns. Center taps will be on each winding at 6, 7 1/2, and 1058 turns respectively. A small chart showing the design considerations of the various windings should now be constructed. This chart should show primary voltage, current, turns, wire size, and the cross-sectional area of the winding. The same data for each secondary also will be shown. The wire insulation also should be indicated for each winding. Returning to our proposed transformer, we found that the core had to have 2.2 square inches of cross-sectional area. We have on hand a core of the shell type, the center leg of which is 1 1/2-inches wide and 1 1/2-inches thick. By removing a few laminations we can bring this core down to 2.2 in cross-sectional area to suit our purpose. The window of this core is 2 1/4-inches long and 3/4-inches wide. It is now our concern to find out if our coil will fit into this window. The window area is 1.688 square inches.

It is now necessary to decide the size of wire to be used for the various windings. In general, the wire should have a cross-sectional area of between 750 and 1500 circular mils per ampere of current to avoid excessive copper losses and to prevent the coil from becoming overheated. By examining a wire table, we find that No. 14 wire has a cross-sectional area of 4107 circular mils, which is acceptable for the 3- and 4-ampere windings. The 1 1/2 ampere winding requires a smaller wire size, so we choose No. 19 wire with a cross-sectional area of 1288 circular mils. The high-voltage winding which carries a current of 0.2 ampere should have an area of about 150 circular mils. We find that No. 28 wire has an area of 151 circular mils, which is satisfactory for our purpose.

Our chart of wire and turns information should now be constructed and for the transformer which we propose to construct, it is shown in Chart I. When we add the last column of our chart we will find the cross-sectional area required for the wire in the coil, in this instance, 0.922 square inches.

An allowance must be made for insulation which should be placed around the core and between the windings. We shall allow 0.050 inch of thickness of insulation for the insulation around the core; as the winding space is 2 1/4-inches long, this means 2 1/44 X 0.050 or 0.11 square inch of insulation at this point. There are four coils to take into consideration, the primary and three secondaries, and between each of these will be inserted 0.025 inch thickness of insulation.

As these coils are again 2 1/44-inches long, this means that this insulation will occupy 0.056 between each pair of coils. As there are four coils with three spaces between them, it means that the insulation between the coils will amount to 0.170 square inch. In addition to this insulation, a cover insulation will be needed to cover the outside of the coil. Let this insulation be 2 1/4-inches long and 0.025 thick; this will occupy 0.06 square inch. Each end of the coil must be insulated. This insulation will be 0.050 thick and 3/4, wide or 0.08 square inch for both ends. The area of the insulation of the coil is the total of all of these individual insulations, or 0.42 square inch for insulation.

Adding this insulation area to the area required by the wire will give the total core window area needed to accommodate the coils. In our proposed design our windings require 0.922 square inches and our insulation requires 0.42 square inch. The finished coil will then require 1.342 square inches. We have not made any allowances for the unevenness and other discrepancies of hand winding or hand construction of the coil. It is necessary to make from 10% to as much as 40% allowance for winding and insulating. If you are careful, the lower percentages will apply, otherwise, the coils should be considered as requiring 30% or 40% of the calculated space requirements. In our present case, we will count on being quite careful and allow 20% for extra space. This 20% of 1.342 square inches is 0.268 square inch and adding this to our computed area we find our complete area, with allowances, is 1.610 square inches. As the window in the core that we have picked for this job is of ample size to accommodate this size of winding we may proceed with our design. (Our window area is 1.688 square inch.)

Chart I - Design considerations of the various windings.

Now find the mean length of turn of each secondary and multiply this mean turn length by the number of turns in each secondary to find the length of wire required for each secondary. This also applies to the primary. Record this length, as it is our purchasing guide for our wire requirements. From a wire table find the resistance per 1000 feet of each size of wire to be used in the various secondaries. Calculate the resistance of the secondary windings. Multiplying the resistance of each winding by the current passing through the winding will give us the voltage drop in each winding. If the voltage drop is objectionable by being too high to give us our desired characteristics of voltage and current then add a few turns to the deficient windings to compensate for this voltage drop. Now square the current of each winding and multiply this by the resistance of each respective winding. This will give a product which represents the I²R or copper loss caused by heat in the windings generated by the passage of current. Note these copper losses and their sum as this factor will be used shortly in computing transformer efficiency. Finding the losses present in the core of the transformer is easily done by calculating the cubical contents of the core, and, knowing that silicon steel weighs 0.27 lb. per cubic inch, we can compute the weight of the core. Of course, it is also an easy matter to put the core on a scale and read the weight if a scale is handy. Our core losses will be about 1.7 watt per pound of core material. Multiply the weight of the core by 1.7 and the result will be the losses in the core in terms of watts. Add these loss figures together with the copper loss and the core loss figures, and their sum will give us the total losses of our transformer.

Take the wattage of the secondaries and multiply it by 100. Divide this product by the same wattage plus the total losses, including both copper losses and iron losses. This will result in a percentage factor which will be the efficiency of the transformer. Stated mathematically:

The efficiency should be about 90% or better. If you have used a smaller wire size somewhere because you had it on hand, you may have increased the copper loss; if the core loss seems high do not reduce the core size, rather use a larger size wire on one or more of the windings to reduce the copper losses.

Lumping all the calculations of our last paragraph for our proposed transformer we find, first, that our mean turn length is approximately 7 inches. There are 270 primary turns, requiring 157 feet of No. 19 enamel wire. As secondary #1 and #2 use the same size wire, we can consider both at one time, and our wire requirement here is 16 feet of No. 14 enamel wire. Secondary #3 will require 1232 feet of No. 28 enamel wire. The resistance per foot of these wire sizes is: 0.002525 ohm per foot for No. 14; 0.008051 ohm per foot for No. 19 enamel; and 0.065 ohm per foot for No. 25 wire. The resistance of the various windings are:

Primary 1.26 ohms; secondary #1, 0.018 ohm; secondary #2, 0.022 ohm; secondary #3, 80 ohms.

The voltage drop in secondary #3 is not objectionable. In order to compensate for our voltage drops in secondaries Nos. 1 and 2, and to overcome the resistance in the leads from the transformer to the sockets, we shall add one turn to each of these windings. Thus, we give them a new value of 13 and 16 turns respectively with the center taps now at 6 1/2 and 8 turns. Change the previously made chart to these new values.

Primary, 2.8 watts; secondary #1 0.16 watt; secondary #2, 0.35 watt; secondary #3, 3.2 watts. The total copper loss is 6.51 watts.

As the core has outside dimensions of 4 1/2 by 3 3/4, inches and weighs 4.6 lbs., the core losses are 7.8 watts. The total losses are the sum of the copper and core losses or 14.3 watts. The efficiency of the transformer is:

Doing the mathematical operations indicated, we find that our efficiency is nearly 91%. As our efficiency figure is our check on the usefulness of our design and our efficiency is over 90% in this case, the design is fully satisfactory and we may go ahead and construct our transformer.

Design Tips for Rewinding Your Own TransformersOctober 1944 Radio News

Design Tips for Rewinding Your Own Transformers
October 1944 Radio News