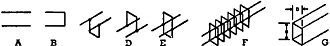Microwave Plumbing Replaces Circuitry |
||
Here is a great treatise on waveguide theory put in layman's language, compliments of Samuel Freedman and DeMornay Budd. Although published in a 1948 issue of Radio & Television News magazine at a time when microwave frequencies were just coming into common use, the language and descriptive drawings are similar to what you will find in modern textbooks. Waveguide is not practical for use at lower frequencies because the physical dimensions are prohibitively large. For instance, for the FM radio band (88-108 MHz), waveguide width for a TE10 cutoff frequency at 88 MHz is around 67.5 inches. According to Wikipedia, the first waveguide was proposed by J.J. Thomson in 1893 and experimentally verified by Oliver Lodge in 1894. * See rectangular waveguide cutoff frequency formula. Thanks to Terry W. for providing this article. Microwave Plumbing Replaces Circuitry
A basic microwave transmitter in its simplest form need be no more than a tube and some microwave plumbing or pipe! To anyone whose past association with radio has been with frequencies below about 1000 megacycles, microwaves are unique in every respect. The basic difference between lower radio frequencies and microwaves is that inductive and capacitive effects are utilized in lieu of coils and condensers. It is achieved by direct action on the magnetic and electric fields through the use of special structures such as simple pipes (called wave guides) of suitable shape and dimension. This is both a necessity and an advantage for microwaves. At conventional radio frequencies, the physical dimensions of inductance in the form of coils or conductors, and of capacitance in the form of condensers are specially provided or "lumped." Their physical size is very small with respect to the operating wavelength. At microwave radio frequencies the physical dimensions of any conductor or condenser are large with respect to the wavelength involved. So little inductance and capacitance is required that the circuit may work best, or only, when "distributed" rather than lumped inductance and capacitance is provided. This may be little more than that represented by the electrodes, their separation, and the connections to the vacuum tube. No wire is efficient in conducting energy at extremely high a.c. frequencies as represented by ultra or super high frequencies. Instead the wire behaves like an a.c. insulator even though at d.c. or low radio frequencies it is an excellent conductor. The reactance or a.c. impedance of any wire or coil increases with increase of frequency. Specifically, it must increase because the inductive reactance in ohms is always equal to: 6.2832 x frequency in cycles x inductance in henrys. Conversely, no condenser is efficient in blocking a.c. energy at extremely high a.c. frequencies because it behaves like a virtual short-circuit or conducting path at microwave frequencies. This is true even though d.c. or low radio frequencies are effectively blocked or isolated by the same condenser. The reactance or a.c. impedance across a condenser decreases with increase of frequency. Specifically, capacitive reactance in ohms must decrease since it is always equal to: 1/6.2832 x frequency in cycles x capacitance in farads. The fact that inductance behaves like an insulator instead of a conductor, and capacitance behaves like a short circuit or conducting path instead of an r.f. block, requires that energy be propagated rather than conducted from point to point even in the case of very short distances within an equipment. The concept now is that d.c. is really a.c. at zero cycles or infinite wavelength. As the a.c. frequency increases from zero, a conductor steadily decreases in its ability to conduct a.c. while a condenser increases. The result is a reversal in radio concepts as the frequencies reach into the microwave region. While propagation of microwave energy in free space is quite conventional for direct paths, it is only during the past few years, even experimentally, that it has been utilized within the equipment itself or for the antenna transmission line system. This propagation technique is achieved by the use of wave guides. Wave guides are simple pipes, usually rectangular, in which one wall simulates the ionosphere and the other wall simulates the earth. The concept is comparable to sky wave propagation on low frequencies in free space. A quarter-wave dipole (miniature at microwaves) at the points of introducing and of extracting the energy may be compared with the transmitting and receiving antennas for lower frequency radio operations in free space. Fig. 2 shows the physical evolution of a wave guide. Fig. 2A shows two wires of any length. It may correspond to the open line shown in Fig. 5. Fig. 2B shows a quarter wavelength shorted line corresponding to the first 90 degrees for the shorted line in Fig. 5. Fig. 2C shows the quarter-wave short of Fig. 2B attached to the open line of Fig. 2A. Note that the point of attachment is the point of maximum impedance for a shorted line a quarter wavelength removed from the short. The current will be zero while the voltage will be maximum at that point. Remember that there is only a.c. sine wave behavior to consider and dimensions are being held correct for the frequency and the wavelength. Fig. 2D shows the same type of quarter-wave short on the opposite side of the parallel wires. Fig. 2E shows the closed loop formed by Figs. 2C and 2D combined. Although it is a d.c, short, it is an open circuit for a.c. because it offers maximum impedance at the point of attachment by virtue of the fact that each shorting section is a quarter wavelength long. A sine energy wave that is maximum at one point will be minimum a quarter wavelength removed. These shorts are really "metallic insulators" much more nearly a perfect insulator than any conventional ceramic insulator could ever be with respect to either d.c. or a.c. Fig. 2F shows a number of loops like that depicted in Fig. 2E. Fig. 2G shows the end result when there are an infinite number of loops so closely spaced that they become a solid pipe. Fig. 3 shows the energy distribution in a wave guide or rectangular pipe. It is necessary to forget the usual conduction principle where a wire carrying a.c. has an associated varying magnetic field encompassing it; or where a varying magnetic field cutting the wire, induces a voltage across the terminals of such a wire. Instead, it is necessary to think of the displacement current principle which requires no wire to carry the energy. It operates on exactly the same principle that electromagnetic waves propagate in free space from a transmitting antenna to a receiving antenna without a physical link between them. The displacement technique operates on the principle that a dielectric or empty space can be substituted for a wire or coil. If the width of the wave guide exceeds a half wavelength and does not exceed a full wavelength in diameter, the wave guide operates on its dominant mode (known as TE0,1) and there will be an energy distribution as shown in Fig. 3. The dominant mode indicates the lowest frequency possible to develop in a wave guide. When the dominant mode is known as TE0,1 (the most common type encountered in practice), it means transverse electric type with the electric field component in the wave guide perpendicular to the axis of the guide. It has no electric component along the length or long axis of the wave guide. 0,1 or 1,0 means that there is one half-wave pattern of electric lines across the cross section of a wave guide along one dimension while there is zero half-wave patterns of electric lines across a dimension at right angles to the first, or vice versa. Note particularly, the following details in Fig. 3:
Fig. 3 - Energy distribution in a rectangular wave guide operated at the dominant or TE0,1 mode. 1. The voltage cancels out at the side walls to equal a total of zero shown by plus and minus meeting at the boundary. 2. The electric field at the center of the wave guide diameter (equidistant from the boundary walls) adds rather than cancels out (plus and plus or minus and minus meet) to result in a sine wave energy distribution as illustrated. This is a simplified form of "Poynting's Vector" to facilitate a graphic portrayal of how the electric component must be zero at the boundaries and maximum between the boundaries but varying in a sinusoidal manner. If the wave guide diameter is doubled for a given wavelength, or if the wavelength is halved for a given diameter wave guide, then in this example, there would be a TE2,0 or TE0,2 mode in which two parallel sets of the pattern illustrated in Fig. 3 would exist. TE3,0 would mean that the wave guide diameter exceeds a wavelength and a half, etc. To avoid multimoding with the energy divided between these different modes or energy patterns, the wave guide diameter must be less than a wavelength. Multimoding may be used where it is not feasible to shrink the wave guide size or lower the frequency. In such event, care must be taken not to couple at a zero energy point. 3. A magnetic field (shown by dotted circular lines) corresponds to the field which would exist around a wire if an electric current were flowing in same. It is distorted to square circles because the wave guide is rectangular in shape. The field alternates in direction each half wavelength in accordance with the sinusoidal characteristic. 4. Energy may be introduced or extracted most efficiently if a quarter-wave dipole protrudes into the wave guide at any point where the electric field is maximum plus or minus in the illustration. 5. Energy may also be introduced or extracted, alternately or optionally, if a small loop is provided in the center of the narrow side of the wave guide pipe so that it couples to the magnetic field. It is immaterial whether a. dipole is used with the optimum position of the electric field or if a loop is used with the optimum position of the magnetic field. Fig. 4 compares propagation in a wave guide pipe on microwaves with that of the ionosphere and the earth from a lower frequency transmitting station. There is little difference between a low frequency radio station propagating long waves in the many miles separation between the earth and .the ionosphere, and a microwave transmitter propagating miniature waves between the two walls of a small pipe. The wave guide pipe will be more efficient and stable since its walls, of good electrical conductivity, facilitate reflection and it is free of changes in dimension due to night and day, seasons or sunspot cycles. The pipe dimensions should be 3" x 1 1/2" at 3000 megacycles, dropping to 1/2" 1/4" at 30,000 megacycles.
Fig. 4 - Free space propagation versus propagation in a wave guide. To propagate energy in a wave guide, it must be below cut-off dimension in wavelength or above cut-off dimension in frequency. If the wave guide dimension in Fig. 4A is less than a half wavelength, energy cannot enter or be accommodated. If it is at "cut-off" or exactly a half wavelength the energy can be accommodated as illustrated in Fig. 4A but it will not make propagational progress down the wave guide's longitudinal axis. Attenuation will be total as the energy will bounce back and forth at one spot, undergoing a loss each time it reflects at a wall. If the wave guide is more than a half wavelength in width, as in the case of Fig. 4B, the energy will make progress at some angle, as shown. The attenuation will go down since there will be less points of contact for reflection to the opposite wall or boundary. If the wave guide width is further increased, the reflecting angle will increase so there will be still less points of contact, further reduction in attenuation losses and greater efficiency in propagation of energy down the wave guide. Fig. 4B might be compared with sky wave propagation at medium frequency while Fig. 4C might be compared with sky wave propagation at high frequency as commonly known for standard and shortwave broadcasting or for amateur radio communication. The principle is similar. The velocity of energy in a wave guide is less than it is in free space for direct path communication. It cannot be 186,000 miles-per-second because the energy takes a zigzag path. Its velocity would only be comparable if it did not have to reflect from wall to wall. It is zero at cut-off (Fig. 4A) and increases as the angle widens out in Fig. 4C. Think of it as 186,000 miles-per-second along the zigzag route illustrated with actual velocity from one end to the other end of the wave guide being its resultant straight line distance. It is comparable to a caterpillar whose wiggles appear to move faster than the progress it is making over the ground. The power handling capacity of a wave guide is much greater than is possible with any practical size conductor. At 3000 megacycles, the 3" x 1 1/2" wave guide can handle over 3,000,000 watts of energy without arc-over between the narrow wall dimensions. Only two opposite surfaces of the wave guide are required. The other two are merely for keeping the parallel surfaces properly spaced. The ionosphere and the earth may be considered as "Nature's wave guide" while the pipes may be called "fabricated wave guide."
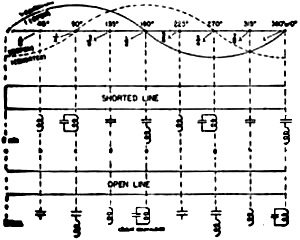
Fig. 5 - Inductive and capacitive effects in a two-wire line or wave guide. (sorry for the lousy image) Fig. 5 shows how wave guide pipe replaces inductance, capacitance, parallel resonant LC or series resonant LC circuits. By moving a dipole probe back and forth through a slit in the wave guide wall, it behaves like a tunable or variable inductance or capacitance. The behavior of an open-ended and shorted line is identical except that they duplicate their phenomena a quarter-wave length or 90 electrical degrees removed from each other. The net result is that the basic microwave transmitter, in its simplest form, need be no more than a vacuum tube and a piece of microwave plumbing or pipe as illustrated in Figs. 1 and 6. This is the same technique developed by Fonda and Freedman which was discussed in the article "Generating Microwaves" in the March, 1947 issue of RADIO NEWS. This particular unit uses a Type 6V6 operating at a choice of frequencies in the vicinity of 2860 megacycles. In this illustration energy coupled by a loop through the wave guide cavity hole shown in Fig. 6 is fed through a calibrated wave guide attenuator to an indicating instrument. The same phenomena and results possible at microwave frequencies may also be realized at any frequency or wavelength as long as the physical requirements prove feasible, and can be utilized. For example, a complete set of events (half wavelength) involves dimension of .2 inch at 30,000 megacycles (1 centimeter wavelength.) The dimension would have to be 20 inches at 300 megacycles (1 meter wavelength). In the broadcast band, at 1000 kilocycles, the dimension would be 500 feet. This statement can be readily appreciated by anyone using an automobile radio on the highway. When the vehicle goes into a tunnel or underpass (even for a few feet), the signal goes dead on the broadcast band while working normally on very high frequencies (such as two-way mobile radio) and still better on microwaves. Microwaves are incomparable for operation in subways or tunnels. Every tunnel, underpass, sides of steel bridges, walls between two sides of a street, two sides of a gorge or canyon etc., forms a wave guide. Energy propagates best there, if at all, when it can accommodate more than a half wavelength for the equivalent of its diameter. Table 1 - Data shown indicates various conditions for shorted and open lines. Reference should be made to Fig. 5 for details on points "a", "c", "e", "g" and "i". The phenomena possible to develop with simple plumbing or mere pipe on microwaves, therefore, make possible results that on lower radio frequencies always require coils, condensers, transformers, resistors, and insulators. These can be eliminated on microwaves by utilizing the inversion, capacitive, inductive, and transformation effects existing along some quarter wavelength of any overall half wavelength for either an open or a shorted line. The impedance in a wave guide may be anything from virtual zero to virtual infinity somewhere along its length. For example, in Fig. 5, there are spotted the conditions and behaviors of Table 1. Any values between those indicated can be developed at intermediate distances. The possibilities for using wave guides are as numerous as applications for the vacuum tube. Both are limited only by human imagination and ingenuity. It only requires that dimensional relationships be correct for the frequency or wavelength employed and the electric and magnetic fields be coupled at the correct point or points for energy introduction or extraction. Fig. 6 - Dismantled view of equipment in Fig. 1. showing a conventional receiving tube used to generate microwaves. The fundamental and harmonic frequencies are masked out because the wave guide dimension is below cut-off for frequencies below about 2800 megacycles. The tube operates at transit time equal to seven periods of oscillation for generating 2860 megacycles in this case. It may be varied by electrode voltages or physical adjustment. 11. Radar where distant objects much larger than the wavelength effectively reflect sufficient energy back to the transmitting source to give indications of distance and direction on a calibrated cathode-ray tube substituted for a loudspeaker. 2. Communications and Relay systems where directivity, channel availability, exceptional bandwidth or privacy are desired. It is particularly valuable tor channels of exceptional bandwidth as required for broadband FM, pulsed or contrast (television) forms of modulation. 3. Microwave Spectroscopy for absorption studies of gases and liquids too rarefied for analysis by the x-ray or the electron microscope. The individual molecules of gases or liquids are sufficiently large in size with respect to the small wavelengths on microwaves to affect the latter propagational characteristics in a wave guide. This can be translated into use-ful scientific or technical information in medical and industrial research. At the present time, communications and relay systems utilize the lower microwave frequencies while radar utilize the medium microwave frequencies and microwave spectroscopy utilizes the highest microwave frequencies.
Posted March 13, 2023 |
||