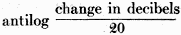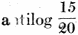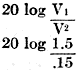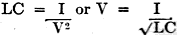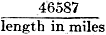The Theory and Construction of Volume Controls, Line Filtersand Matching
Transformers |
|
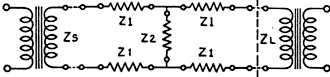
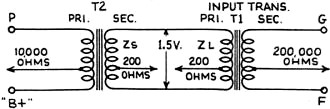
Here is Part 1 of a three-part article on attenuator pad and impedance matching articles that appeared in Radio-Craft magazine. Although the focus is on audio frequencies, the principles apply in general. It is interesting to read about wavelengths expressed in units of miles versus feet and meters like we are used to seeing for radio frequencies. Keep in mind that most of the decibel formulas used here are for voltage and not for power. The Theory and Construction of Attenuators, Line Filters and Matching Transformers (Part I) The Theory and Construction of Attenuators, Line Filters and Matching Transformers (Part II) The Theory and Construction of Attenuators and Line Filters (Part III) The Theory and Construction of Attenuators, Line Filters and Matching Transformers (Part I) By Hy Levy, B.S. In any well-designed voice transmission circuit, such as telephone lines, radio-broadcast speech equipment, public-address systems, "talkie" apparatus, etc., will be found resistance networks, or attenuators, more commonly called "pads." The proper use and design of these pads make for an efficient transmission system, from which the maximum output of energy with the least distortion may be obtained, and which, if these pads were not used, could not be realized. It can be said that pads find their way into practically every phase of voice transmission where quality reproduction is the prime requisite. It is the purpose of this article to make clear the methods by which these pads are designed, to show their application in transmission circuits, and to discuss the problems encountered in transmission circuits where pads are used. Purpose of Pads In voice-transmission circuits, where energy is being transmitted over a line to a load located at the far end of the line, it is necessary that some means be employed to control the magnitude of the energy entering the load. It is for such purposes that pads are used. These networks are always used between a source of energy and a load. The source of energy might be any of the following: (1) Output of a speech amplifier, such as a normally high-level amplifier which is feeding another amplifier located at a remote point; (2) Output of a high-level am-plifier (power amplifier); (3) Output of a low-level amplifier, such as a condenser-microphone amplifier, which is feeding a speech amplifier located at some distant point; (4) Output of microphone circuits, etc.: The load may consist of a transmission line carrying the energy and terminating in an impedance located at the far end of the line. This load impedance might consist of any of the following: (a) Primary side of a line-matching transformer (line to line transformer); (b) Input circuit of a speech amplifier; (c) Loud speakers located at distant points from an amplifier; (d) Mixing circuits, etc. The attenuator imposes a constant impedance upon the transmission line, thereby controlling the level (magnitude) of the energy being transmitted into the far end of the line. The attenuator or "pad" maintains this level by introducing a loss in energy between the source and the load, at the same time causing no impedance mismatch to the impedances between which it is working (source impedance and load impedance). To illustrate the statements given in the preceding paragraphs, a typical case showing the use of such networks will be given. The complete design and calculation of the pads will be shown, and the problem arising in circuits in which these pads are used will be discussed. It is hoped that by obtaining a complete understanding of the subject matter given in these papers, any problems relating to the design and use of pads in voice transmission circuits will be materially lessened. Let us assume we have a radio amplifier whose output voltage is 1.5 (effective value of alternating current). This voltage is to be fed over. a transmission line, at the far end of which is located the primary side of an input transformer, whose secondary is in the input circuit of an amplifier (see Fig. 3). Let us also assume that it is also necessary to reduce the voltage impressed across the primary side of the transformer to approximately 0.15 volts (R.M.S.). It can be seen, therefore, that it is necessary to interpose a network of some sort between the input source of 1.5 volts and the primary side of the input transformer in order that the voltage will be reduced to the desired value, at the same time introducing no impedance mismatch between the source and the load. In voice transmission circuits, this network is composed of non-reactive resistances so arranged that they will cause the desired loss between the input and output terminals of the pad. By "non-reactive" is meant resistances whose impedance remains practically constant to alternating current. This is accomplished by constructing the resistances so that their inductance and capacitance is negligible throughout the frequency band in which they function. (The construction of the resistances for use in the pads will be given in a forthcoming article). For most purposes, this frequency band can be taken as the audio spectrum of 40 to 10,000 cycles per second. The resistances used in networks must be non-reactive in order that the attenuator maintain constant impedance characteristics throughout the audio band to the impedances between which it is working, so that straight line frequency attenuation will be obtained without frequency distortion in the transmission circuit, which would hinder the intelligibility of the signal. The change in voltage between the source and the load is expressed as the logarithmic ratio between the two voltages. At this point a brief resume on the transmission unit or decibel will be given, so that those not familiar with this unit will have a clear understanding of how it is used in transmission circuits. In electrical circuits carrying energy which is either being amplified or attenuated, the question arises: What is the relationship between voltage, current, and power on the input side of an amplifier or an attenuator, to the voltage, current, and power on its output side? The engineer signifies this ratio between two voltages, two currents, or two powers, by the number of decibels change taking place between the input and output terminals of the amplifier or the attenuator. The Decibel In any electrical circuit carrying energy, the product of the common logarithm of the power ratio multiplied by ten, or the product of the common logarithm of the current or voltage ratios multiplied by twenty determines the change in decibels. As an example of this principle, let us assume that in a certain circuit the voltage has been decreased from 3.0 volts to 1.0 volt, or to one-third of its original value, Then from the definition as given above, the voltage ratio is 3 to 1, or 3. The common logarithm of three is 0.4771 (which may be obtained from a table of common logarithms). This means that 0.4771 is the power to which ten must be raised to give three. Then, multiplying 0.4771 by twenty, we get 0.9542 decibels change: i. e., decibels change = where V1 = input voltage and V2 = output voltage
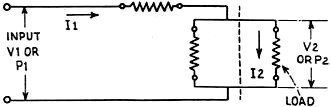
= = 20 log 3.0 = 20 X 0.4771 decibels change = 9.542 The above simply means that if the voltage in the circuit has been decreased to .one-third of its original value, we have caused a change of 9.542 units or decibels to have taken place. (See table in November, 1931 issue of Radio-Craft - Editor.) This change in decibels is expressed as. a loss, as the voltage has been decreased. Similarly, if the voltage had been increased to three times its original value, the resultant change in decibels would also be 9.542, only in this case the result would a gain. Therefore, if the voltage has been increased or decreased to three times its original value, the resultant change in decibels is the same in both cases, or 9.542. The only difference in the two cases is in the method of expressing the results obtained. When using the formulae shown below, the change in decibels obtained depends on the type of circuit involved. In an amplifying circuit, the relationship between the voltage, current, or power ratios is expressed as a gain in decibels. In an attenuator, the relationship between the voltage, current, or power ratios is expressed as a loss in decibels. In the circuits to be taken up, attenuators (resistive networks) will be discussed, and a decrease in energy will be incurred between the terminals of the pad, and therefore all results will be given as a loss in decibels. Thus by expressing current, voltage, and power ratios in decibels, one has an accurate description of the changes in energy taking place in the circuit. From the definition of the decibel as given above, we can write the following formulae: Change in decibels = where P1 = input power P2 = output power V1 = input voltage V2 = output voltage I1 = input current I2 = output current This is shown in Fig. 1. Also if we know the number of decibels change, and it is desired to determine the voltage, current, or power ratios, we can write: To illustrate this method, assume we wish to introduce a 15 decibel loss into the circuit, and it is desired to know what voltage ratio will give this loss. Then from above: which means that if the voltage ratio is equal to 5.62, a 15 decibel loss will be maintained in the circuit. Returning now to our own problem, it was determined that a network is required to cause a loss in voltage between its terminals, from 1.5 volts, on the input side, to 0.15 volts, on the output side. This loss expressed logarithmically is as follows: loss in decibels = = 20 log 10.0 = 20 x 1.0 loss in decibels = 20.0 or, a 20 decibel loss is to be incurred between the input and output terminals of the network to be designed. This is the same as saying that by reducing the voltage from 1.5 volts to 0.15 volts, or in the order of ten times, a loss of twenty decibels has taken place. The first problem to be considered is what type of network shall be used to cause this loss in voltage. In communication circuits, two types of networks used for this purpose are: (1) "H"-type pad (2) "T"-type pad The H-type pad will be discussed first, and a complete discussion will be given showing the method of obtaining the desired twenty decibel loss by the use of this pad in our own problem. The H-type pad is so called because it is composed of five resistances taking the form of the letter "H". This pad is designated as a balanced network, in that an equal number of resistances (Z1) are used in the series arms on both sides of the line as shown in Fig. 2. In some circuits, the shunt arm Z2 may be divided into two equal parts, with the midpoint grounded. This balances the entire network with respect to ground. At this point an investigation of certain factors which must be considered in transmission circuits will be given in order that an understanding of the problems encountered in voice transmission will be bad. It is of the utmost importance that a general knowledge of the circuit characteristics be obtained, so that when the design of the pads is taken up, maximum efficiency may be obtained from the transmission line in which the pad is to be placed. In Fig. 3 is shown the output circuit of an amplifier feeding a transmission line, at the far end of which is located an input transformer T1. The transformer (T2) used in the output circuit of the tube is called a tube-to-line transformer or output transformer, in that it transfers energy from the tube to the transmission line. The secondary side of this transformer is called the source impedance of the line, for the energy induced in this winding is the energy transmitted along the line. This transmission line, we can assume, terminates in the primary side of an input transformer (T1), whose secondary side is in the grid circuit of a vacuum tube. This transformer is called a line-to-tube transformer or input transformer, as it transfers the energy from the line into the tube. The primary of this transformer is known as the load or terminating impedance, as the transmission line can be considered as ending at this point, for the primary side completes the transmission line, and the secondary side is considered in another circuit. In communication circuits the source and load impedances of the transmission line have been standardized in most cases to 200, 500, and 600 ohm lines. Therefore. if ZS, the source impedance, equals 200 ohms, then the load impedance ZL must also equal 200 ohms in order to prevent so-called "reflection" losses from being set up in the circuit. It is these "reflection" losses that will now be discussed. Reflection Losses The speed with which electromagnetic waves travel is the same as that of light, or approximately 186,000 miles per second. This speed is attained only in a circuit having zero losses, which of course is not obtainable in practice. All circuits have some losses, and in transmission lines these losses increase as the frequency increases. The speed of the transmitted waves is retarded slightly by the losses of the line, and by what is known as "skin effect" of the line conductors. (Skin effect is the forcing of the current to flow along the outer surfaces of the conductors.) As the frequency increases, the inductance inside the conductor (mostly in the center) increases, thereby offering a greater opposition to the flow of current within the conductor, and consequently the current is forced to travel along the outer surface of the wires. The relationship which exists between inductance, capacitance, and the velocity of light is: where V = velocity of light in miles per second L = inductance in henries C = capacitance in farads If a frequency of 100 cycles per second is impressed upon a circuit of infinite length (no end), at the end of 1/1000 of a second the wave will have traveled 186000/1000 or 186 miles. A part of such a wave is shown in Fig. 4. This circuit is said to have a full wavelength for the frequency of 1000 c.p.s. (cycles per second). In this circuit, when the first part of the waves arrives at a point 186 miles distant from the start of the transmission line, the end of the. same wave is at the start of the circuit. This is assuming zero losses in the line. The actual wave would be slightly retarded due to the losses of the circuit. This is shown in the dotted lines of Fig. 4. If now an alternating-current wave is impressed upon a transmission line, it will travel along the line with the speed of light, until it reaches the far end of the line, where, if the far end is open (infinite impedance), the wave will be reflected back to its origin with the same velocity, but will gradually decrease in magnitude as it approaches the starting point of the line, due to the losses of the line which it encounters. If at the moment this wave reaches the starting point another wave is sent into the line, that which was left of the first wave adds itself to the second wave and therefore increases the second wave. If, at the moment that the returned second wave reaches the starting point, a third wave is sent into the circuit, that which was left of the second wave adds itself to the third wave and so on as the number of waves increases; with the result that an accumulative effect of energy is developed in the circuit. The magnitude to which this reflected energy can rise is determined by a characteristic of the line conductors known as the "surge impedance." The surge impedance of a conductor is the impedance which the conductor offers to these free oscillations of energy at the high frequency limit. (This condition is greatest at the highest frequency that the circuit passes.) This building up of reflected energy in the circuit is known as "quarter-wave resonance," or merely as the resonant frequency of the line. To produce such a condition, it is necessary that the alternating-current impulses occur at intervals of time equal to the time necessary for the energy to travel the length of the line and back. In other words, for one complete cycle (two impulses) the energy would have to travel the length of the line four times between successive impulses in order to create resonance. Expressed as a formula:
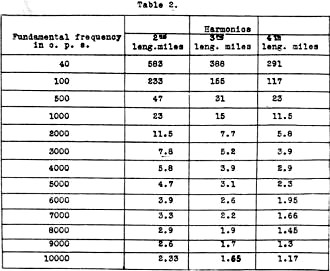
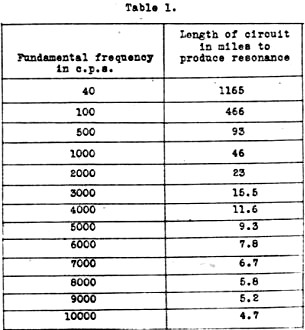
frequency = or, length in miles = It can be seen, therefore, that as the frequency increases the length of the circuit becomes shorter in order to produce the resonant condition. In table 1 is given the length of circuits in miles to produce resonance throughout the audio band. At this condition of resonance, the magnitude of the reflected energy reaches a maximum; and abnormal voltages and currents are set up in the circuit. This reflected energy, if present in a circuit in which vacuum tubes are employed., will cause incorrect voltages to be applied to the grids of the tubes, which in turn will cause distortion of the wave-form of the of the original signals, with the result that harmonics will be generated in the circuit. As these harmonics increase, the resonant period of the circuit is decreased. This is shown in table 2, where the resonant periods of circuits due to harmonics being set up in the line are given. It can readily be seen that as the harmonics increase, the length of the line necessary to produce resonance is decreased. Now in practical circuits, such as the transmission lines encountered in everyday sound work, the resonant condition may not be theoretically reached as the fundamental frequencies used are not high enough to produce resonance for the length of the lines ordinarily used, which in most cases are comparatively short. Nevertheless, if the lines are not properly terminated, the reflected energy which is set up produces distortion of the wave-form of the original impulses, which in turn will create harmonics. These harmonics are multiples of the fundamental frequencies, and as these harmonics increase, the frequency of the circuit increases, thereby approaching the resonant frequency of the line. .Consequently, as the resonant period of the line is approached, extreme distortion of the signals arises, with the result that the quality is atrocious. Mechanical Analogy The analysis of reflected electrical waves is analogous to that of water flowing in a canal. If the near end of a canal is struck a blow, a water-wave will be set up which will travel to the end of the canal, where it will be reflected back to the origin. As it travels back toward the starting point, its amplitude will decrease slowly, due to resistance encountered in the canal. If, at the instant the wave reaches the origin, another blow is struck, a second wave will flow to the end of the canal and return. This second wave will be composed of itself, plus that which was left of the first wave. This effect increases as the number of waves is increased, and reaches a maximum when the losses due to resistance prevent the amplitude of the waves from increasing further. If a gate or obstruction of some sort is inserted at the end of the canal, any waves traveling down the canal will strike the wall and bank up to a height determined by the potential energy of the wave. When the potential energy equals the kinetic energy impressed on the wall, the wave will have reached its maximum height. It can be shown that in certain cases the waves will rise to a height twice that of the original wave striking the wall, and then will be reflected back at a slowly decreasing amplitude as the starting point is approached. Similarly, in electrical circuits, when an electromagnetic wave reaches the end of a transmission line, and the line is open at the far end as shown in Fig. 5, the wave is reflected back to the source; the current is zero, and the voltage at the load reaches a value equal to twice the peak value of the original voltage. Also, if instead of open circuiting the far end of the line, it is short circuited, the wave is reflected with a current value twice the value of the starting current, and the voltage becomes zero. This is shown in Fig. 6.
Posted August 18, 2020 |
|

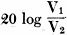
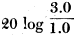
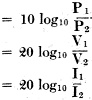
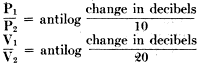
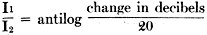
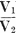 =
=