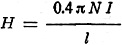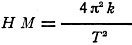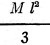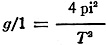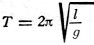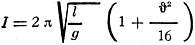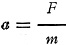|
September 1942 Radio-Craft
 [Table
of Contents]
Wax nostalgic about and learn from the history of early electronics.
See articles from Radio-Craft,
published 1929 - 1953. All copyrights are hereby acknowledged.
|
Buckle your mental seatbelt
before reading this fast-moving rundown of the origins of many measurement standards
used in the cgs (centimeter-gram-second) system. It reminds me of a video you might
see of a physics dude "wowing" an audience of science laymen as he rolls through
one topic after another, among them being mass, acceleration, time, electricity,
magnetism, solenoids, pendulums, inertia, and gravity. There's nothing you haven't
seen and heard before in the first couple chapters of Physics 101 class in the way
of equations and drawings, but you'll probably enjoy the review. It appeared in
a 1942 issue of Radio-Craft magazine.
Standards of Measurement
Fig. 1 - Helmholtz coil.
By Willard Moody
If you go back and try to find out what an ampere, volt or ohm really is, you
will ; find that electrical and mechanical units of energy, or work, are defined
in terms of the fundamental quantities, distance, mass and time. Work will be done
by the moving of a mass in a unit of time. A gram moved a distance of one centimeter
in one second is a definite amount of work done, equal to the basic unit of work;
the erg. This represents the centimeter-gram-second system of measurement, abbreviated
c.g.s.
Time is determined by astronomical observations. The sidereal day is reckoned
by the interval of time between successive meridian passages of the same star. This
is the time required for earth rotation of one cycle. The solar day is reckoned
by the motion of the sun. When the sun is on the meridian, it is said to be solar
or apparent noon. The interval of time between two successive noons represents the
solar day. The average length of the solar day over a. period of one year is the
mean solar day. The second will be 1/86,400th part of this day.
The centimeter is 1/100th part of the meter. In 1799 a platinum bar was constructed
by Borda for the French Government which had a length of 1 meter, the meter being
taken as 1/10,000,000th part of the meridian line from equator to the pole. It is
now known that this distance is 10,000,856 meters, but the original bar serves as
the standard.
The gram, unit of mass, is 1/1,000th part of the kilogram, The gram is equal
to the mass of a cubic centimeter of pure water at 4 degrees Centigrade. The standard
kilogram is a bar of platinum kept at Paris and is the real standard on which all
metric weights are based. The unit of mass in engineering is the pound, which is
equal to 453.59 grams.
The gram has been defined in terms of the centimeter, gram and second. The centimeter
and second have been explained in detail. The remaining factor is the 4 degrees
Centigrade specification. Melting ice will represent 0 degrees on the Centigrade
scale, and the temperature at which water boils under standard atmospheric pressure
will be 100 degrees on the Centigrade scale. Now, what is standard atmospheric pressure?
It is the pressure of one atmosphere, derived from a column of mercury 76 centimeters
high at zero degrees Centigrade. In sound measurements, of radio engineering, the
bar is occasionally used. A bar is 1/1,000,000th part of the pressure corresponding
to 75 cm. of mercury at zero degrees Centigrade.
Now we come to the unit of force. The Greek word for force is dyne. A force of
one dyne acting on a mass of one gram will change the mass velocity by one centimeter
per second. In other words, the force required to
move [accelerate*] 1 gram a: distance of 1 cm. in 1 second is 1 dyne. The work
that is done and the energy used up or expended is 1 erg.
In magnetism, a unit pole is one which if placed 1 cm. from an equal pole in
vacuum will repel it with a force of 1 dyne. The relation, stated mathematically,
is  where m is the magnetic
strength of the first pole and m' is the magnetic strength of the second pole. The
factor rp is the distance between poles in centimeters. The strength
of the magnetic field at any point is the force in dynes on a unit magnetic pole
placed at that point. When a pole of strength m is placed at a point where the field
intensity is H, the pole is acted on by a force Hm dynes. In any field of force,
the two poles of a magnetic needle are urged in opposite directions. The direction
in which the north pole tends to move is known as the positive direction of the
line of force at that point.
In electrostatics, unit charge or unit quantity of electricity is defined as
that quantity which when placed 1 cm. from an equal charge in vacuum repels it with
a force of 1 dyne. Stated mathematically,
 where q is the first
electrostatic unit and q' is the second electrostatic unit. The factor r is the
distance between the charges, measured in centimeters.
In electromagnetics, unit current is that current flowing in a circular coil of
1 centimeter (cm.) radius which will act on a magnetic pole at its center with a
force of 1 dyne for every centimeter of wire in the coil.
The practical unit of electricity is the Ampere, named in honor of the French
physicist who investigated current. The quantity of charge transmitted by 1 ampere
in 1 second is called a coulomb. One coulomb is equal to 3,000,000,000 units of
electrostatic charge, as defined previous to the definition of electromagnetic charge.
In electromagnetics, 1 volt potential difference exists between two points when
unit current is moved between the two points by energy equal to 1 erg. The volt
is 100,000,000 electromagnetic units of potential. The practical unit of resistance
is equal to 1 volt divided by 1 ampere.
Electromagnetic field strength is measured by force per unit pole and is a vector
quantity having both magnitude and direction. The magnetic field is indicated by
drawing as many lines of force per sq. cm. as the field has units of intensity.
The magnetic flux is equal to the magnetomotive force divided by the reluctance.
If in a magnetic circuit there are 1,000 lines of flux, there are 1,000 Maxwell's.
The Maxwell was named in honor of Clerk Maxwell, English physicist. In a moving
conductor which has induced in it 1 electromagnetic unit of potential, the flux
cut per second is 1 Maxwell. The unit of induction is the Gauss and is equal to
Maxwells/cm.2 In other words, in a magnetic field having 1 line per square
centimeter, or 1 Maxwell per cm.2, there is 1 gauss or unit induction.
Magnetic intensity induction or flux density B is measured in lines of magnetic
induction per square centimeter (gauss). If the substance in which the field exists
is non-magnetic, B is the equal of H and the ratio B/H or permeability is μ =
1. When the substance through which the field passes is magnetic (say iron core
placed inside of an air core solenoid) B becomes much greater than H, in a relationship
which seldom is linear and must be determined experimentally for a given material.
The number of flux lines of force will be equal to 
The reluctance of an iron ring may be calculated:
where 1 is the length of the ring A the cross sectional area and μ the permeability
constant of the iron.
The French physicist Arago, in 1820, demonstrated electromagnetism. The attraction
of the armature to the magnet poles, expressed in dynes, is:
 (pull per sq. cm.
of pole area)
The energy of a magnetic field is
Fig. 2 - Magnetic pendulum swing angle.
Fig. 3 - Tangent Galvanometer
Fig. 4 - The Pendulum
The intensity of a magnetic field H at a point is equal to the magnetic potential
gradient at that point. The average intensity of field between two points may be
considered the average fall of magnetic potential all along the path and is expressed
in oersteds or gilberts/cm2. In a long straight solenoid with length
25 times the diameter.
where H = oersteds, field intensity ( vicinity of center)
l = centimeters, coil winding length
N = number of turns in coil
I = current, amperes
A Helmholtz coil may be used for determining field intensity in a certain plane,
as illustrated in Fig. 1.
The magnetic force of the solenoid, at any point inside of it, is for Fig. 1
expressed by the relation:
The intensity of the horizontal component of the earth's magnetic force may be
measured by the following method due to Gauss. A small steel bar magnet is suspended
horizontally by a fine silk thread in a closed box which protects it from air currents.
It is then set to oscillate through a 5 degree arc or swing and the period of oscillation
is carefully determined by using a stop watch. This period depends on M, the magnetic
moment of the magnet and on H the horizontal component of the earth's magnetic force.
This is expressed by the relation,
where k = is the moment of inertia of the magnet, which depends upon the size,
mass and shape.
To determine the relation of H and M, a second procedure is necessary. Suppose
that (in Fig. 2) P is the point where the magnetic intensity H is to be determined.
A short magnetic needle is placed at P, while the magnet bar is placed exactly east
or west of P, and with its axis on the east-west line. If r is the distance from
the center of the bar to P, the force at P due to the bar is,
Then at P the force due to earth and the force due to the magnet bar are represented
vectorially. The tangent of the angle will be F/H or 2M/r3H and H/M then
equals 2/r3tanθ. M may also be determined by the Helmholtz coil.
But, since F/tanθ = H, knowing the product of H and M, the quantity H can
be divided into that product to get M. The Helmholtz coil or the magnetic needle
and bar methods are used for determining H. The moment of inertia k is given by:
Moment of inertia =
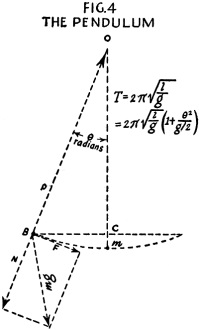
where M is the mass in grams and 1 the length in centimeters of the magnet bar.
The tangent galvanometer shown in Fig. 3 can be used for determining absolute
electromagnetic unit current. The coil is large compared with the magnet needle,
so that the poles of the needle are considered as being at the center of the coil.
The cross section of the coil must be of large enough mean radius so that all turns
bear essentially the same relation to the needle.
The pendulum may be used for the establishment of frequency. The action is shown
in Fig. 4. We may assume the whole mass of the pendulum to be concentrated
at B, the mass of the silk cord being so small as to be negligible. The forces acting
on the mass m are its weight mg and the tension P of the suspending cord. The weight
mg may be resolved into two components, one in line with the cord and opposing its
tension and one at right angles to the cord and in the direction in which the mass
m moves. The latter component F, gives the mass a motion through the arc. The force
diagram is then BCO, and
F/mg = BC/BO
As BO = 1, the length of the cord, and the angle through which the pendulum swings
is quite small, BC is practically equal to arc BA. The arc length of BA may be represented
as x. Approximately,
F/mg = x/1 and
F = mgx/1
Therefore the force F persuading m along the arc toward A is proportional to
the displacement x measured along the arc. This is a simple, harmonic vibration
expressed by the relation of force to period of vibration in the equation,
substituting, we have:
and 
(g = acceleration due to gravity)
The period of vibration is dependent only on length of the pendulum and acceleration
due to gravity at the place the pendulum is swung, and is independent of its mass
and length of arc if the length of arc is small (say 5 degrees). A more exact formula
is:
Where the arc is measured in radians, between points A and B.
The values of gravitational constant for various locations are given in the following
table. The height is assumed as being at sea level.
Pole 983.1 cm.2 sec." or 32.25 ft./sec.2
London ............ 981.2
32.19
Paris ................ 980.9
32.18
New York ......... 980.2
32.16
Washington ..... 980.0
32.15
Equator ........... 978.1
32.09
An approximate formula due to Clairaut gives the gravitational constant at n
latitude and h height above sea level.
g = 980.6056-2.5028 cos 2n-0.000003h
The force urging downward a freely falling m is shown by the equation,
F = mg
where F is force in dynes, m mass in grams and g the gravitational constant in
centimeters/sec.2. The force unit in poundals, weight of 1 pound falling,
is 32.16 poundals at New York latitude. The standard force of a pound may be stated
as the weight of a pound mass at New York, where the acceleration due to gravity
happens to be 32.16 ft./sec.2. The acceleration due to a constant
force acting on a mass moving in a single direction is constant and is related as
in the equation,
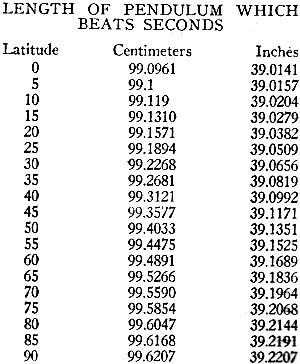
Length of Pendulum Which Beats Seconds
It should be realized that mass and weight are not identical. The unit of mass
is a physical quantity of arbitrary size, chosen as a constant. One c.c. of water
at 4 decrees Centigrade represents one gram of mass. The engineering pound is 453.59
grams. If we take a mass of one gram, raise it to a height of n centimeters above
ground level, and then allow the mass to fall freely taking the time with a stop
watch for the fall to be completed, we have a means of determining the velocity
constant of gravity at the point on the earth where the experiment is conducted.
Speed is the ratio of unit length to time. We have miles/hour, ft./sec. and cm./sec.,
etc., so that if. S = 1/2 gt2 and we know the speed and time, we can
compute readily the gravitational constant. Conversely, knowing the gravitational
constant, we may figure the speed of a falling object.
If we have a standard of mass and time and know the height above sea level we
can determine the latitude. If we have an accurate standard of height above ground,
such as a fine rule or scale graduated in inches we can measure the time required
for an object to fall a certain distance and the gravitational constant will then
be 2s/t2 where s is the speed.
* Thanks to RF Cafe visitor Marek Klemes, Ph.D., for catching this error
in the original article!
Posted August 24, 2022
(updated from original post
on 10/28/2014)
|
