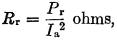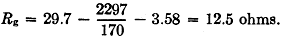Short Antennas for Mobile Operation |
|
Here is a very in-depth and comprehensive discussion on antenna system design and evaluation for a mobile platform; i.e., a car or truck. As was common with QST articles of yore, there is a plethora of equations, sketches, graphs, and tables provided for reference. Radiation resistance, ground resistance, system impedance, antenna tuning, radiation efficiency, current distributions, and much more are introduced and explained. Even being six decades old, the information is as valuable today as it was then. Short Antennas for Mobile Operation Loading the Whip for Low Frequencies By J. S. Belrose, VE3BLW Many of those who have 75-meter mobile installations do not understand that if all of the power output from a mobile transmitter could be fed to a short whip, almost 100 per cent of it would be radiated. The problem in getting power into the antenna is definitely one of eliminating losses in the system. In this article, VE3BLW discusses the various points ill the antenna circuit where these losses are introduced and how they can be minimized.
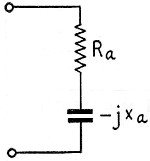
Fig. 1 - Equivalent circuit of a short vertical radiator. Seventy-five-meter mobile radio operation is becoming quite popular both in Canada and in the United States. Many types of antennas have been used, such as simple base-loaded whips, center-loaded whips, top-loaded whips having disks, metal balls, or spoked wheels, and folded antennas. Several articles have been published in QST1, 2, 3 on low-frequency antennas for mobile use. However, the exact operation of a short vertical antenna is not too well understood by a good number of those using the antenna. I would like to try to explain clearly, on a mathematical basis, the operation and design considerations for a short antenna. The fundamental frequency of a vertical radiator is the lowest frequency for which the reactance is zero at the customary feed point - between the lower end of the radiator and ground. At this frequency, the electrical length of the antenna is 90 degrees, or a quarter wavelength. Vertical radiators which are short electrically have low radiation resistance and relatively high capacitive reactance. At frequencies near the operating frequency the antenna can be considered as being a lumped circuit which consists of a resistance and a capacitance in series, as shown in Fig. 1. Here, Ra is the total antenna resistance, which includes principally the radiation resistance and the ground-loss resistance, and Xa is the capacitive reactance of the antenna at the operating frequency. It is clear that in order for this antenna to take power, the capacitive reactance of the antenna must be tuned out by a suitable inductor. The inductor introduces additional resistance, and the object in design is to obtain the highest practical ratio of radiation resistance to loss resistance. In what follows, I propose to analyze the radiation efficiencies, bandwidths, and practical construction of base-loaded and center-loaded whip antennas. The expected range, for ground-wave propagation, is discussed, and it is shown mathematically that a better range is possible using 160 meters rather than 75 meters. Definition of Radiation Efficiency The total useful power radiated from an antenna can be considered as being that which would be dissipated in a fictitious resistance with the antenna current, at the point of reference, flowing through it. Normally, the current is measured at the base of the antenna, and therefore the radiation resistance is referred to the base of the antenna. Pr = Ia2Rr watts, where Pr = power radiated, Ia = antenna current, and Rr = radiation resistance. The radiation efficiency of an antenna is the ratio of the radiation resistance to the total resistance of the antenna system.
where Rr = radiation resistance, Rg = ground-loss resistance, and Rc = tuning-coil-loss resistance. Under proper conditions, insulator-loss resistance and conductor-loss resistance can be neglected. Since the loss resistances are generally greater than the radiation resistance, for short antennas, careful design must be used to engineer a usable antenna system. Radiation Resistance The radiation resistance of a vertical antenna less than an electrical quarter wavelength is increased by top loading and by increasing the height. For short radiators, it can be shown that4 Rr = 0.01215A2 ohms, where A = degree-ampere plot of current distribution on the antenna.
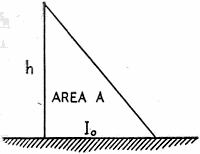
Fig. 2 - Current distribution on a short vertical antenna. Consider the current distribution on a short vertical radiator. The current will be some value, I0 at the base of the antenna, and zero at the top of the radiator. If the antenna is very short - less than 30 degrees - the current distribution can be assumed to be linear. This is shown in Fig. 2. For example, assume that h = 110 inches (2.79 meters), f = 3.81 Mc. (78.6 meters). Then, Gv = electrical height of antenna in degrees
So = 6.4 degree-amperes, and Rr = 0.01215(6.4)2 = 0.5 ohm.
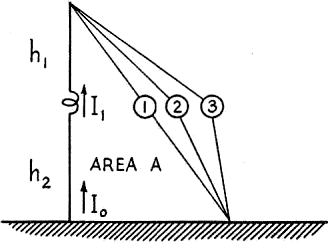
Fig. 3 - Current distribution on a sectionalized or center-loaded antenna. Now consider the effect of introducing a series loading coil, as shown in Fig. 3. If the inductance of the loading coil is zero, the current distribution will be curve (1), as shown in Fig. 3. This is obviously that of a simple base-loaded radiator, as shown in Fig. 2. As the inductance is increased from zero, the current distribution is modified to that of curve (2). At some value of inductance, L0, the input impedance of the antenna as seen between the base of the antenna and ground is a pure resistance with no reactive component. For this value of inductance, L0, we have the maximum current area on portion h2. This is shown as curve (3) of Fig. 3. For this condition, the current flowing through L0, I1 = I0 cos G2, where G2 = electrical height of h2 in degrees (similarly G1 = electrical height of h1) For example, assume that h1 = h2 = 55 inches (1.4 meters), and G1 = G2 = 6.4 degrees (at 3.81 Mc.). Hence, I1 = I0 cos 6.4° = 0.995 I0
= 9.57 degree-amperes, and Rr = 0.01215 (9.57)2 = 1.11 ohms. It is clear that a considerable increase in the radiation resistance is obtained by placing the inductance in the center portion of the radiator. Ground-Loss Resistance
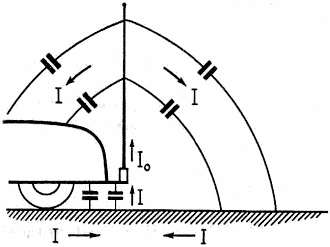
Fig. 4 - Current loop for a vertical radiator mounted on a car. The current flowing at the base of the antenna must be returned to the base of the antenna by currents induced in the ground beneath the radiator. These currents must be collected by the car body and through the capacitance of the car body to the ground. Since the area of the car body is considerably less than a quarter wavelength, only a portion of these currents will be collected by the car frame itself, and the rest will be collected by ground currents flowing through the capacitance of the car to the ground. Since the ground is not lossless, quite a large loss resistance, Rg, is found. The current path is shown in Fig. 4. In the past, writers have neglected this loss resistance. This resistance will be a function of the positioning of the radiator, the type of car on which the antenna is mounted, and to some extent on the ground beneath the radiator. A value of 10 to 12 ohms has been measured by the author for 8- to 16-foot antennas at 3.8 Mc. Tuning-Coil-Loss Resistance In order that a short antenna will take power, the capacitive reactance of the antenna must be tuned out by means of a suitable tuning coil. To estimate the inductance required, we need to know the capacitive reactance of the antenna at the operating frequency. The reactance of a short vertical antenna, such as shown in Fig. 2, is
h = average height of radiator above ground, a = average radius of radiator, and Gv = electrical height of radiator. For example, let us calculate the reactance of the base-loaded antenna shown in Fig. 5. Fig. 5 - Vertical radi-ator mounted on a car.
a = 0.125 inch,
and Gv = 12.8° (at 3.81 Mc.) (Add 5 per cent for spurious end effects.)
A tuning coil of 73.4 μh. is required to supply an equivalent positive reactance at 3.81 Mc. If the coil has a Q-factor of 300, then
Now consider the sectionalized antenna, as shown in Fig. 3. Firstly, we calculate the reactance of the top portion. From this we subtract the lumped reactance of the loading coil, and finally the input reactance of the antenna is calculated by assuming the lower portion an opened-out transmission line, terminated in the resultant reactance of the loading coil and the top section. If the antenna is resonated so that the base reactance is zero, it can be shown that the reactance of the inductor required is jXL0 = jZ0 (cotan G1 - tan G2) ohms, where Z0 = characteristic impedance of antenna (as before), G1 = electrical length of top portion of antenna, and G2 = electrical length of bottom portion of antenna. For example, suppose we have the antenna system of Fig. 6.
a = 0.125 inch, Z0 = 418 ohms (as before), and G1 = G2 = 6.4° (at 3.81 Mc.) (Add 5 per cent for spurious end effects.) jXL0 = j418 (cotan 6.71° - tan 6.71°) = j3500 ohms, or 146.3 μh. at 3.81 Mc. If a coil with a Q-factor of 300 is used, the coil-loss resistance,
Bandwidth of Antenna System
Fig. 6 - Center-loaded whip mounted on a car. For frequencies near resonance, the antenna may be considered as a lumped circuit with a Q-factor of
where Rt = total antenna resistance. The operating bandwidth of the antenna is therefore approximately
For the vertical base-loaded whip described, Rt = Rr + Rg + Rc = 0.5 + 10 + 5.85 = 16.35 ohms. For the center-loaded antenna described,
It must be remembered that a bandwidth of 5 kc. is required for double-sideband a.m. 'phone operation. The bandwidth of both antennas described above is adequate. However, the proximity of near-by metal objects can cause considerable detuning of the circuit. Also, very little shift in operating frequency can be allowed without retuning the antenna. Theoretical Radiation Efficiency The radiation efficiency of an antenna was shown to be the radiation resistance divided by the total resistance, or
For the 110-inch base-loaded whip,
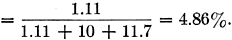
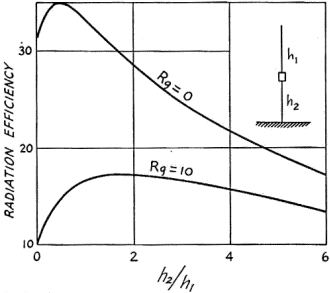
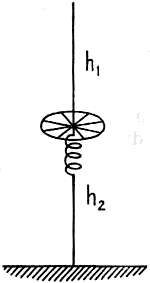
It is clear that a small but worthwhile improvement is obtained by center-loading the antenna. However, this is gained at the expense of reduced operating bandwidth, and increased mechanical-construction problems. Determination of the Optimum Location of the Loading Coil Suppose we have a 16-foot whip antenna. The antenna is bumper-mounted, the base insulator being 2 feet from the ground. The average radius of the radiator is 0.18 inch. We decide to load this antenna by introducing a loading coil in series with the antenna, and would like to know where this coil should be placed for maximum radiation efficiency. If we choose a coil Q-factor of 300, and a ground resistance of 10 ohms, the graph in Fig. 7 shows the calculated variation of radiation efficiency with the ratio h2/h1. The ratio h2/h1 = 0 is, of course, the case of a base-loaded antenna. It is seen that the best location for the coil is approximately in the center of the radiator (or h2/h1 = 1). The curve for no ground-loss resistance is also shown. It is noted how the optimum location of the coil is shifted toward the feed point as the ground-loss resistance is reduced. Field Measurements of Radiation Resistance The actual measurement of radiation resistance of an antenna at 3.81 Mc. is difficult, and involves equipment not normally available to the average amateur. However, to show that measurements. can be taken to prove the theory we have developed, I think a short discussion of the principles involved would be in order. The surface-wave field intensity (that is, for grounded radiators) from a short radiator can be expressed in terms of radiated power, distance, and propagation factor for the ground between the transmitter and receiver by the following expressions:
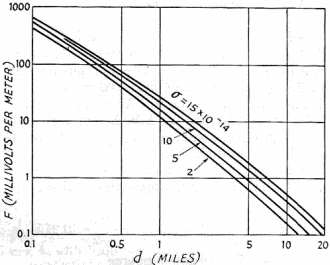
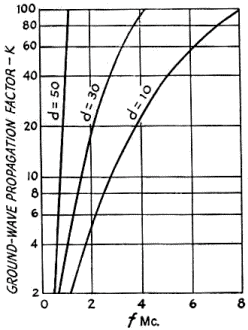
where F0 = unattenuated field strength at one mile in millivolts-per-meter, k = propagation factor to take account of ground conductivity, dielectric constant of the ground, and diffraction due to curvature of the earth, d = distance in miles, F = field strength received at distance d, and Pr = power radiated. Fig. 8 - Graph showing variation of ground-wave field intensity with distance for poor to good ground. σ = ground conductivity, Frequency = 3.8 Mc. Ground dielectric constant ξ = 15. The first step necessary in order actually to measure the radiation resistance of the antenna is to determine how the ground influences the electric field. To determine this, we must make several measurements of the field strength at distances out to at least 10 miles from the transmitter. In this way a graph showing field strength against distance can be plotted. Comparison with a set of theoretical curves, as shown in Fig. 8, after Norton,5 is then made. In Fig. 8, several curves are shown ranging from poor ground (σ = 2 X 1014) to good ground (σ = 15 X 1014). The propagation factor, k, is the ratio, at distance d, of the unattenuated or inverse-distance field strength, divided by the actual field strength predicted by the curve for a particular ground conductivity. Once the power radiated is found, then the radiation resistance,
where Ia = base current. This is obvious, since the actual power radiated can be considered as being the real power dissipated in a fictitious radiation resistance. Measurements on an Actual Antenna A sectionalized 16-foot antenna was built. h1 = 6.86 feet, h2 = 9.29 feet, a = 0.18 inch, and f = 3.81 Mc. The antenna was bumper-mounted on a 1940 Dodge sedan, the base being 272 feet above the ground. Suppose we design a suitable coil so that the input impedance at 3.81 Mc. is a pure resistance. 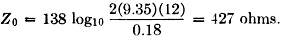
A coil 2 inches in diameter was wound with 66 turns of No. 14 enameled wire. The inductance was found to be 97.6 μh. with a coil Q-factor of 170. This was installed. The resonant frequency was found to be 3.81 Mc. with an input resistance of 29.7 ohms. This was measured with a General Radio r.f. bridge type 916-A, an Eddystone receiver type 750, and an A.V.O. signal generator. The equipment was battery-operated and isolated from ground. To calculate the radiation resistance, refer to Fig. 3. Substituting in appropriate values, 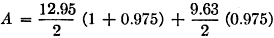
Therefore, the ground-loss resistance must be
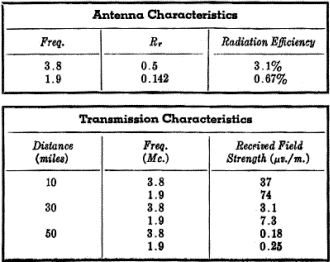 To check the calculated figures, the field intensity was measured 0.284 miles from the antenna using a Stoddart field-intensity meter type NM-20-A. Preliminary measurements indicated a ground conductivity of 10 X 10-14 The results are as follows: f = 3.81 Mc., F = 3.5 mv./m., d = 0.284 miles, k = 2.06 (see Fig. 8 where a = 10 X 10-14), and Ia = 0.185 amperes. Hence, F0 = Fkd = 3.5(2.06)(0.284) = 2.04 mv/m, 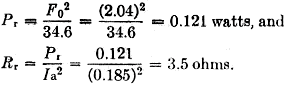
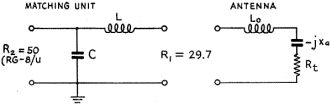
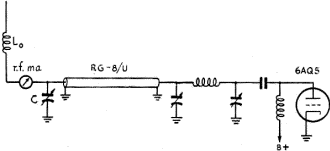
The agreement of measured with calculated values for radiation resistance is better than normally experimentally obtained due to the many parameters involved. It is noted that the radiated power is 0.121 watt. The power input to the antenna was supplied by a single Type 6AQ5 tube and is Pin = (0.185)2 29.7 = 1.01 watts. This corresponds to a radiation efficiency of 12%. Tuning and Matching Center-Loaded Whips A method of matching the antenna to the transmitter will now be considered, and a method outlined by which the antenna can be tuned using a g.d.o. and an s.w.r. detector (equipment normally owned by the average amateur). Firstly, let us consider what matching involves. If we consider the 16-foot antenna just discussed, the input impedance at resonance was a pure resistance equal to 29.7 ohms. We must transform this low value to 50 ohms so that the antenna can be fed with standard coaxial cable (RG-8/U or RG-58/U). This can be done with an L-section matching unit as shown in Fig. 9.
Substituting values, 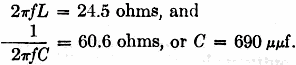
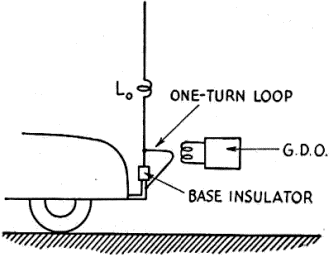
Now the inductance, L, can be artificially obtained by adding just a small amount more inductance to L0 the center-loading coil, than needed for resonance, thus making the antenna input impedance inductive. An exact match to 50 ohms can be obtained by adjusting the condenser, C, and the center-loading inductance, L0. First, resonate the antenna by a. g.d.o. as shown in Fig. 10. Power is coupled into the antenna from a 50-ohm transformer. In my case the output tank circuit is a pi-tank. See Fig. 11 for set-up. Adjust the condenser, C, in small increasing steps, resonating each time by adjusting the center-loading coil for maximum current. For some value of C near 690 μμf the antenna will draw maximum current and show no detuning effects at the transmitter end. An s.w.r. detector will also indicate a minimum s.w.r. for this adjustment. (Note: L and C of Fig. 9 can be reversed. A small coil could be used instead of condenser C. The coil should have an inductance of 2.45 μh. - i.e., 60.6 ohms. The antenna must be tuned slightly capacitive. That is, resonate the antenna alone as before, and subtract turns from L0 to resonate again after introducing the small matching coil. This method has certain advantages, and its use should be considered.) Summary
Fig. 12 - Adding more capacitance. In conclusion, I hope that I have made clear the factors involved in antenna design and also the considerations in matching the antenna to 50 or 70 ohms so that it can be fed with standard coaxial cable. It is shown that some improvement can be obtained by center loading - a gain of 1.5 in power - but this may not always be worthwhile since the mechanical problem of fixing a good high-Q coil in the center of the whip is difficult. The diameter-to-length ratio of the coil should be 2/1 if possible. The placement of a spoked-wheel-type disk, as shown in Fig. 12, could be used to provide a substantial reduction in the size of the loading coil required. For example, a 1-foot-diameter ring of No. 12 with eight spokes has a capacitance equivalent to the length of the radiator h1 for the experimental 16-foot antenna discussed. However, it is felt by the author that such means are not adaptable to mobile antennas, since cumbersome structures like this are rather sorry-looking sights after striking a tree branch at 50 miles per hour. Choosing the Optimum Frequency Let us consider whether it would be better to use 1.9 Mc. rather than 3.8 Mc. At first thought, one might say not, since the antenna efficiency will be much lower. However, the lower ground-wave propagation factor overcompensates for this. The variation of the propagation factor with frequency and distance is shown in Fig. 11 for good ground (σ - = 10 X 10-14) If we assume a transmitter power of 50 watts, an antenna as shown in Fig. 5, coil Q-factors of 300, and ground-loss resistance of 10 ohms, the results for transmission over 10, 30, and 50 miles are shown in the accompanying tables. Fig. 13 - Graph showing variation of propagation factor, k, with frequency and distance for good ground (i.e., conductivity σ = 10 X 10-14, and dielectric constant ξ = 15). Distance d is in miles. It is seen that at all distances the received field strength is better at 1.9 Mc. than at 3.8 Mc. It is also interesting to note that the atmospheric noise level goes through a broad minimum near 2 Mc., which is another factor in favor of using 1.9 Mc. The field strength required to communicate varies with the time of day, season, frequency, and location. For frequencies near 1.9 Mc., approximately 0.5 μv./m. is required at noon for radiotelephone communication in Ontario. Many times that is required at night - 30 μv./m. at 8 P.M. in the summer, and 100 μv./m. at the same time in the winter. These estimates were taken from graphs given in Laport.6 It would be interesting if a few amateurs decided that 75-meter 'phone is too crowded and moved down to 160 meters. I will bet a lot more would soon move down after comparing cross-channel transmissions at distances up to 50 miles. This, of course, is so only if there is no sky wave, such as a summer day. Normally low-power mobile operators on the low-frequency amateur bands communicate by ground wave.
1 Oberlies, "Installing a Practical 75-Meter Mobile Antenna," QST, Dec., 1949. 2 Swafford, "Improved Coax Feed for Low-Frequency Mobile Antennas," QST, Dec., 1951. 3 Wrigley, "Folded and Loaded Antennas," QST, April, 1953. 4 Laport, Radio Antenna Engineering, p. 23, McGraw-Hill (1952). 5 Norton, "The Calculation of Ground-Wave Field Intensities Over a Finitely-Conducting Spherical Earth," Proc. I.R.E., 29, 623 (1941). 6 Laport, Loc. cit., p. 542-555.
Posted July 28, 2016 |
|

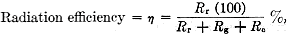
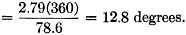
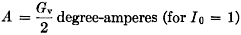
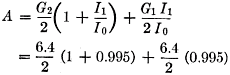
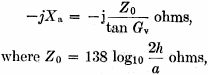
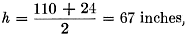

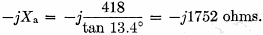
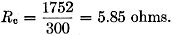
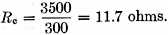
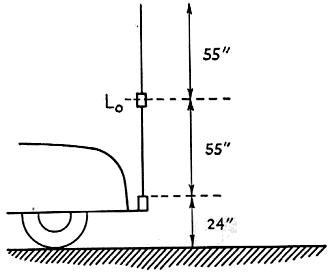
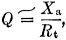
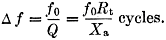
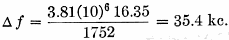
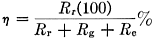
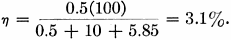 For the 110-inch center-loaded whip,
For the 110-inch center-loaded whip,