Note on Reduction of Distortion and Noise with Inverse Feedback
|
|
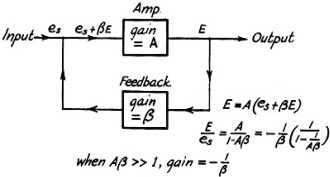
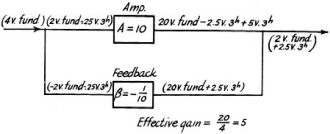
Feedback circuits seem simple enough intuitively, at least for simple systems. It is easy, though, for someone not comfortable with algebraic manipulations to arrive at the wrong conclusion for how a given feedback constant figures into the calculation. Such was the case with an article published in the July 1937 issue of ARRL's QST magazine, when many readers wrote to the author accusing him of making an erroneous claim in an earlier article (April) regarding using feedback to cancel out an unwanted harmonic in an amplifier. The criticism turned out being justified. Here is a statement of the error and an explanation of the proper approach which was printed a couple months later. Note on Reduction of Distortion and Noise with Inverse FeedbackA few of our readers have disagreed with some of the conclusions reached, with respect to optimum inverse feedback conditions for reduction of distortion and hum, in the article describing the construction of a speech-amplifier-modulator unit in April QST.1 Since the criticisms are all of the same nature, we have selected for publication a letter from J.R. Davey, New York, which gives a rather complete explanation of the operation of the inverse feedback circuit in this respect: "The section of the article headed 'Curing Distortion and Noise' contains several statements which I believe to be incorrect. The author begins this section by showing how a 5-volt third harmonic in the 20-volt fundamental output of the amplifier used as an example is eliminated by using a feedback ratio of 1:10. A feedback ratio of 1:10 and a stage gain of 10 would actually cut the distortion and noise introduced in the stage to one-half its original value, and not eliminate it completely. "The author also applies the same reasoning to the hum elimination problem, reaching the general conclusion that the feedback ratio should be the reciprocal of the gain of the stage. Here again this actually gives a reduction of 50 per cent in noise, distortion and the effective gain of the stage. The statement that it this ratio is exceeded overcompensation would result, and that the distortion would increase, is quite incorrect. As the negative feedback is increased, the noise, distortion, and effective gain all continue to decrease. To get complete cancellation of the noise and distortion would require infinite negative feedback and consequently zero gain. The error in the reasoning is that it neglects the fact that as soon as the noise or distortion is cancelled out in the output by some means, there is no longer any signal component to feed-back and continue the cancellation. "There also appears to be an inconsistency in that there is first mentioned the possibility of overcompensation and then later that the theoretical ratio of gain of stage is a minimum value and that larger amounts may be used. The actual feedback ratio used in designing an amplifier depends on how much gain it is economical to lose, how much feedback can be used without excessive positive feedback and oscillation at the extremes of the frequency range, and the amount of noise, distortion, or potential supply variations which are being compensated for. There is a feedback ratio in each case beyond which there is no point in going, either because of loss of gain, phase difficulties, or because a closer approach to the desired response characteristic would not be warranted. "The usual type of nomenclature used in feedback amplifiers is given in Fig. 1. It is to be found in numerous publications treating the subject. "The reduction of gain caused by the feedback is 1/(1-Aβ).2 This is also the reduction in noise and distortion produced in the stage.3 The characteristic with feedback approaches that of the feed- back or β circuit. When, as in this article, β = -1/A, the factor 1/(1-Aβ) becomes 1/2. The above factor is demonstrated below in obtaining the table given on page 47, April QST: "The actual case of the author's distortion example is shown in Fig. 2. The 5-volt third harmonic produced in the amplifier is reduced one-half, to 2.5 volts, but not eliminated. If Aβ should be made as high as 15 to 20, then much more reduction of distortion (1/16 and 1/21) would be obtained. I have no doubt that the amplifier as described works very well, but there appears to be no foundation for the desirable feedback ratio of 1/gain of stage." 1 Carter, "Inverse Feedback Applied to the Speech Amplifier for the Amateur 'Phone Transmitter," QST, April, 1937. 2 When the feedback is negative, as is the case here, β is negative. - Editor. 3 The amount of distortion fed back to the grid circuit is equal to β times the resultant distortion in the plate circuit; i.e., the distortion remaining in the output with feedback present. The resultant distortion is the algebraic sum of the original distortion without feedback and the amplified feedback distortion. Letting D = resultant distortion with feedback and d = original distortion without feedback. D = d + ADβ Solving this for D, D = d/(1-Aβ) See Terman, "Feedback Amplifier Design," Electronics, January,1937. - Editor
Posted June 30, 2023 |
|