A Passive RF Limiter |
||||||||||||||||
This passive limiter is a simple combination of cascaded "T" type resistive attenuators that are switched in and out of the circuit based on the power level in the line. The design takes a bit of thinking due to needing to retain a reasonable impedance match at the input and output throughout various stages' conduction states. Arriving at an optimal value for resistors would require a circuit simulator with a mathematically based optimizer, but, especially for amateur radio work, close is good enough. That is not to say Hams are a bunch of slackers - they're not - it's just that component and software resources are not as readily available (aka "prohibitively expensive") for doing the analysis and testing. In 1966 when this article was published, software did not even exist for people without access to university or corporate computers. For most users these days, it is cheaper to buy a limiter for 2- to 3-score dollars from suppliers like Pasternack, Mini-Circuits, and others. Note the distortion apparent in the limited waveform. A Passive RF Limiter
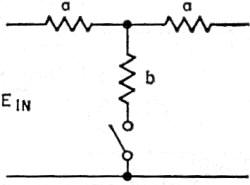
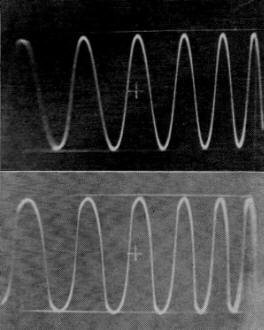
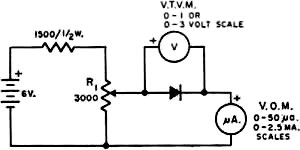
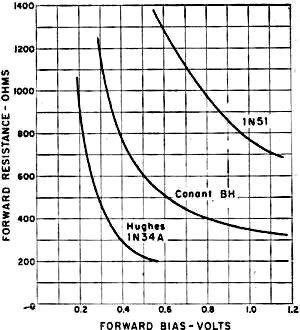
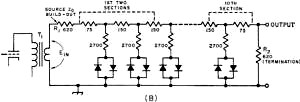
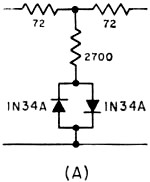
Fig. 1 - The basic limiter circuit. Closing S1 increases the attenuation without changing the frequency-transmission characteristics. S1 should close when Ein reaches a predetermined value. These scope pictures show the effect of limiting on waveform. (A) Sine wave (765 cycles) before limiting; (B) Same signal after 8 db. of limiting. By George Schleicher.* W9NLT An interesting audio limiter circuit using diode switching of resistive attenuators. It does not "slice the top off the signal" sharply the way simple diode clippers do, and thus has relatively little effect on the bandwidth of a speech signal. A limiter circuit can be constructed with passive elements; the design of this one is such that it will not generate high-order harmonics and it need not be frequency sensitive in the audio range. The limiter uses a multiplicity of T-section attenuators in tandem; each section is unusual in that a pair of diodes is connected in series with the shunt arm. The diodes function like switches that open in the absence of a potential but close when the voltage applied to any section of the attenuator rises to a predetermined level. The closing of the shunt path causes the loss of the attenuator section to increase to its design value. The switching action is illustrated in Fig. 1. As a result of the switching action each section of the attenuator will offer a small loss to the low-amplitude portion of an electrical signal and a higher loss to amplitudes of higher level. The maximum loss of any attenuator section is governed by its design. The maximum amount of compression that the limiter can provide is determined by loss of each attenuator section and the number of sections that are connected in tandem. Good results have been obtained by using ten or twelve sections in tandem, each section having a maximum loss of two or three decibels. The maximum amount of compression that will be realized from a limiter of this type will be equal to about half of the total loss of the attenuator sections. When a voice signal is modified by limiting action there is necessarily a change in the harmonic relationships within the signal. Listening tests indicate that heavy limiting using a limiter of this type causes a voice signal to become somewhat "bassy," but this effect is hardly noticeable if the voice signal has been limited to a bandwidth of only 3 kc. by means of a filter. Diode Action Solid-state diodes exhibit resistance in the forward conduction mode. This resistance can vary from a fairly high value (over 10,000 ohms) to less than 100 ohms. It will depend on the voltage across the diode and the materials of which the junction is made. The materials also determine the manner in which the diode will begin conduction. For example, copper-oxide junctions begin conduction more slowly than germanium or silicon. Design Principles The characteristics of the diodes and the design of the attenuator sections should be complementary. The diode resistance when conducting should be low enough to be negligible in the shunt arm of the attenuator; in the nonconducting mode it should be high enough to make the shunt appear as an open circuit. Pairs of diodes are used so that the positive-going and the negative-going portions of a wave will be similarly affected. The voltage at which the diodes begin conduction determines the range over which the limiter will be effective. The limiter circuit should be driven from a source having an impedance at least as high as the design impedance of the attenuator sections, and it should be terminated in a similar impedance. Since the diodes are connected in the shunt arm of the attenuator the basic limiter design can be applied to both balanced and unbalanced (one side grounded) attenuators. The circuit described here uses unbalanced T sections for simplicity. Fig. 2 - Test setup for measuring diode resistance. R1 is a linear control. Fig. 3 - Resistance of three types of diodes measured with the test circuit shown in Fig. 2. Fig. 4 - (B) Cascaded sections; note that the 75-ohm series arm on the output side combines with the 75-ohm series arm on the input side to make the single value of 150 ohms between adjacent shunt arms. Half-watt resistors are satisfactory. In this circuit T1 is assumed to have a turns ratio such that the plate resistance of the preceding amplifier tube is transformed to a value of resistance that is low compared with the characteristic impedance, 600 ohms, of the attenuator. Likewise, the input impedance of the device to which the limiter is connected is assumed to be high compared with 600 ohms. When this is not true, R1 and R2 should be selected so that total input and output impedances are 600 ohms. A Practical Circuit
Fig. 4 - (A) Practical circuit for a single section. Building a limiter of this kind can start with the acquisition of about two dozen diodes of a given type. Their forward resistance should be measured using an arrangement similar to that shown in Fig. 2. Measurements should be made in increments of 0.05 or 0.1 volt starting at zero and continuing until the current through the diode reaches its maximum rated value for the type of diode under test. A graph can then be drawn plotting junction voltage against resistance (resistance is first computed by dividing the voltage by the resultant current). Fig. 3 shows the kind of curves that result when different diodes are measured this way. Using the curve for the 1N34A as an example, it is evident that the resistance will drop to about 200 ohms and that there is a "knee" in the curve at a potential of 0.45 volts. The potential is significant because it corresponds to the input voltage at which limiting action is maximized. The diode resistance at the knee (250 to 300 ohms) is used in designing the attenuator sections.1 The shunt resistance used in the attenuator should be about ten times the diode resistance at this point, or 2700 ohms if the nearest standard resistor value is chosen. Knowing that the shunt resistor will be 2700 ohms and desiring a loss of about 2 db. in the attenuator leads to the conclusion that the characteristic impedance of the attenuator should be 72 ohms. (These conclusions are arrived at through the help of the formulas given below.) The resulting limiter circuit is shown in Fig. 4. It should be noted that between attenuator sections the output series resistor of one section has been combined with input series resistor of the following section (72 + 72 = 144 ohms). Again the nearest standard resistor value (150 ohms) has been chosen for use in the circuit. The waveform photographs show how compression changes the shape of a sine wave. Appendix Attenuators are lossy resistive networks. They are usually designed to have the same impedance at their input and output terminals. Unbalanced attenuators are usually referred to as "T" or "π" attenuators since these letters describe the circuit configuration. Their balanced counterparts (for use in ungrounded circuits) are referred to as "H" or "O" attenuator Only four simple formulas are needed in designing T attenuators; they are as follows: Loss (expressed in db.) =
n = a (the series resistor value) =
b (the shunt resistor value) =
(Z is the characteristic impedance of the attenuator). As an example of the use of these formulas, assume that you are designing an attenuator of 150 ohms impedance with a loss of 6 db.: 6 = 6/20 = 0.3 =
Fig. 5 - Attenuator used as an example for calculation as described in the Appendix.
{antilogarithm of 0.3 = 2.0} from slide rule or log table 2.0 =
a = 150 b = 150 A single attenuator section of 150 ohms impedance and 6 db. loss is shown in Fig. 5. Some representative attenuator section values are shown below. They are included as an aid in designing limiters of the kind described here. These values are based on an attenuator impedance of 1000 ohms. For other impedances the values should be increased or decreased proportionately. 1 The resistance measured in this way is a "d.c." resistance, and while for higher accuracy in circuit design the dynamic resistance should be determined, its measurement is considerably more difficult. The extra complication would not be warranted unless it were necessary to know the exact attenuation at different voltage levels.
Posted April 29, 2021 |
||||||||||||||||

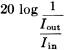 {1}
{1}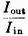 {2}
{2}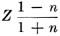 {3}
{3}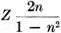 {4}
{4}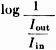 {from 1}
{from 1}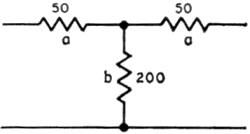
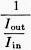
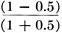 = 150
= 150
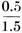 = 50 ohms
{from 3}
= 50 ohms
{from 3}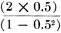 = 150 (1/0.75) = 200
ohms {from 4}
= 150 (1/0.75) = 200
ohms {from 4}