Modeling Radiation Patterns of Whip Antennas
January 1967 QST

Computer modeling of antenna radiation patterns has evolved from a relatively simple electric field equation that diminishes as the inverse of the distance from the source, to exotic, highly sophisticated numerical methods that account for conducting and dielectric surfaces and volumes. A spreadsheet can be built rather quickly to calculate and graph the free-space azimuth and elevation e-field patterns for a 1/4-wave whip or a dipole antenna using textbook formulas, but building a model for displaying the 3D radiation patterns of a cellphone placed next to a human head, or a UHF radio antenna on top of an aircraft takes some pretty serious computing power. In large part we owe a debt of gratitude to the Ph.D. types who have labored hard to make such tools available to us commoners. As with PCB layout software and circuit simulators, chances of success with a first pass prototype has increased significantly as software has improved. Even with the advent of near-miraculous software, there is still a need to verify empirically that the design matches the predicted results. That's where taking physical measurements comes in. Fortunately, there is a lot of great software for automating testing as well, but occasionally, especially for the less well funded amongst us, measuring points manually is required. Even with automated systems at your disposal a few quick "sanity check" points are measured prior to submitting the design to a full barrage of tests. This article describes how the author first calculated the expected pattern for a 1/4-wave vertical whip antenna mounted on a car, and then went about validating his predictions.

Modeling Radiation Patterns of Whip Antennas

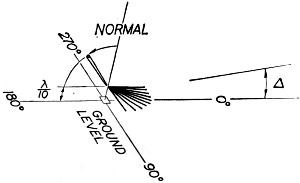
By Dale W. Covington, K4GSX

The rapid development of efficient transceivers and power supplies has solved many of the problems of going mobile. Furthermore, old Sol is playing a strong supporting role by improving propagation conditions on the very bands for which the mobile antenna is most efficient. While the bandwidth and efficiency of the whip antenna have been extensively studied and improved, any description of the resulting radiation patterns has received only light treatment. Such patterns would be useful guides, for example, in calling DX or in beginning to conclude a contact before making a major change of route direction. Therefore the intent of the following note is to call on stage yet another actor portraying a simplified picture of mobile whip radiation.

Actually it is a complicated matter to describe this radiation precisely as a function of the total elliptical polarization of the radiated E-field, the distorted currents flowing on sculptured car bodies and loaded whips, the frequency dependence of the ground conductivity, and so on. On the other hand, the principal features can be exhibited by using a model of a vertical element over an incomplete ground plane.

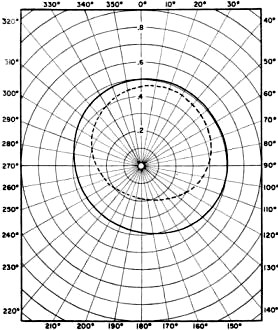
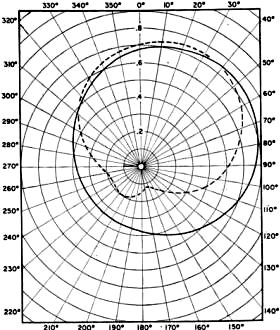
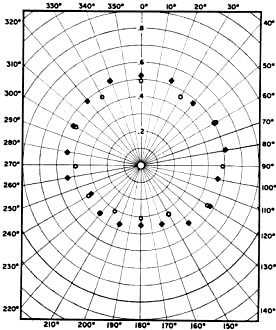
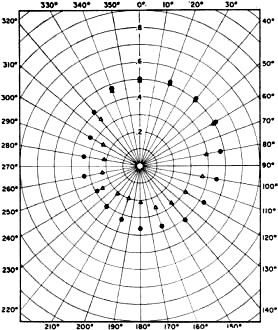
The Model

Employing a model for a complicated analysis usually implies a certain degree of approximation. The case in point is no exception. Cars are about 1/4 wavelength long at 20 meters and almost 1/4 wavelength wide at 10 meters. As the whip itself is a 1/4 wavelength at 10 meters, it seemed appropriate to restrict the analysis primarily to this 10- to 20-meter range. Fig. 1 shows the general shape and the coordinate position of the model, which had ten 1/4-wave ground radials from 0 to 90 degrees beneath a vertical 1/4-wave element fixed in the normal-180-degree plane. The ground plane was spaced 1/10 wave above ground. Crudely speaking, the model thus represented a car with a whip mounted on the left rear deck. The driver's side is along the 0-degree direction, and the rear bumper is along the 90-degree direction.

Patterns

The actual calculation of the patterns consisted of computing the far E-field from cosinusoidal currents flowing on 1/4 wave elements¹ as arranged in Fig. 1. All of the resulting vector fields were then added to yield a polar plot of the radiation patterns as a function of the angle of elevation. Since an actual whip does not remain truly vertical once the car starts moving, the equations for the model were solved for the vertical element normal to and tilted away from the ground radials.

The close spacing between the model and ground requires that ground effects be included in the analysis. A review of the interrelations between frequency, antenna height above ground, angle of elevation, and ground constants has been given by G3HRH^{(note 2)}. Using standard techniques³ the E-field expressions were corrected by the ground factors for 28 Mc. and angles of elevation, Δ, of 15 and 30 degrees. Higher wave angles are less useful for contacts from 14 to 28 Mc.⁴. These ground factors revealed that, at their maximum point, the horizontally polarized E-fields from the model over dry soil were 11.7 and 5.9 db. below the corresponding vertically polarized fields for Δ of 15 and 30 degrees respectively. As the conductivity approached sea-water values, the horizontal terms were even smaller: namely, 14.2 and 8.3 db. For simplicity only vertical terms were retained in the patterns.

The patterns of the calculated E-fields are presented in Fig.  2 for the 15- and 30-degree wave angles. Solid lines show the fields from the vertical element normal to ground while the dotted lines denote a rather extreme element tilt of 45 degrees. The relative field strengths can be directly compared from one wave angle to the other; however, directly comparing field values of the normal and tilted configurations automatically implies a constant input current. It is immediately noted in Fig. 2 that the quadrant containing the ground plane also contains the strongest fields. Moreover, these fields generally change only slightly from 0 to 90 degrees.

When the vertical element is perpendicular to the radials, the field pattern is symmetric about the 45-225 degree directions. Here orientation is more important at the high elevation angle where the pattern undergoes a maximum/ minimum variation of 6.4 db. compared to a 3.3-db. variation at the lower angle. As mentioned before, the attractive increase in field strength at the higher angle usually cannot be advantageously employed on the higher-frequency bands.

Pattern symmetry becomes lost as the vertical element tilts back from the normal. Not only does the direction of maximum field shift from 45 degrees toward 20 degrees, but also the field strength from the rear of the model is particularly reduced. Numerically the fields in front of the model are 8.3 and 13 db. stronger at the 15 and 30 degree elevations.

Low-Frequency Considerations

Mobile operation on 40 and 80 meters is more difficult to analyze. Even in Texas cars and whips don't come equipped with 1/4-wavelength dimensions. Instead, the sizes of both the car body and the whip approach small fractions of a wavelength. Also, in this range the loading coil becomes increasingly important in relation to the current distribution on the whip. Finally, contacts can be made on these bands by radiation at fairly high angles of elevation, which complicates the previous polarization argument by filling in certain parts of the pattern with a significant combination of vertically- and horizontally-polarized fields.

The relative directivity pattern for a very small dipole has only a slightly greater beam width than the similar figure-8 pattern for a half-wave dipole having 1/4-wave elements⁴. Thus it would be reasonable to expect that the character of the patterns of Fig. 2 would be more nearly omni-directional because of the short length of the radiating elements. Consequently this factor along with the increased usefulness of the higher angles of elevation would reduce any directivity effects for 80- and 40-meter mobile contacts.

It is interesting to speculate about the patterns predicted by the model for an incomplete ground plane installation at a fixed station. On the lower bands, particularly, it is not always practical to extend the long ground radials in a symmetric shape about the base of a vertical antenna. The model should be useful in understanding such cases if the obstruction limiting the ground plane to less than a circle does not likewise prevent the vertical element from being installed in the clear. For example, the patterns for a vertical installed at one corner of a garden would probably differ from those for a vertical next to the corner of a house, even though both conditions might have a 90-degree area that was unavailable for ground radials. Basically, the model suggests that a hole or depression exists in the radiation pattern centered in the area having no radials. Directly opposite the hole is centered a broad field maximum over the ground radials. The hole is a function of the angle of elevation, and its maximum depth is of the order of 6 db. or so below the field in the opposite direction at elevations near 40 degrees. Naturally the hole width could be greatly reduced as the area about the base is more evenly covered with radials.

Experimental Results

The computed patterns were subjected to several checks. One check utilized an experimental model of Fig. 1 at 430 Mc. The wire model was located about three wavelengths from a two-element beam fed by a 6J6 rig from an old Handbook design. The detector was a 1N23 crystal operating in the square-law region. The measured E-field pattern is given in Fig. 3A for the vertical element perpendicular to ground and an angle of elevation of 15 degrees. There is good general agreement with the calculated pat-tern of Fig. 2A. Tilting by 45 degrees produced a maximum/minimum gain of 5 db. An increase of radiation in the forward directions was noted at higher elevations.

Of course the primary reason for examining the incomplete ground plane model lay in the degree that it approximated 10-20 meter mobile radiation. Included in Fig. 3A is a mirror image (whip mounted on right rear fender) of some 20-meter E-field data taken on the mobile installation of WA4KQO. While the receiving antenna was higher than the whip-Hillman combination, the angle of elevation unfortunately was not measured. It was less than 5 degrees. The experimental points are characteristic of the low-angle radiation from the model.

To further confirm the effects of tilting the whip away from the normal, a 1/15.4 scale model of a Toronado was constructed. At this scale, the 430-Mc. whip was equivalent to a 1/4 wave whip on 10 meters. An aluminum foil skin 0.00125 inches thick covered the balsa stringer shell. Fig. 3B presents the measured field strengths at a 15-degree wave angle. Input power remained constant as the whip was tilted. Again comparing the experimental data with the curves of Fig. 2A, it is apparent that the ground-plane model does agree fairly well with the scale model. Indeed, the standard deviation of the measured points was 1.2 db. for both the normal and tilted conditions.

Conclusions

The radiation patterns of a 1/4-wave ground plane model have been employed to approximate the patterns from a mobile whip in the 10-20 meter range. For these bands the operating experiences of several mobile hams indicate that the field strength over the car body is on the average 3 to 6 db. stronger than the field in the opposite direction. This magnitude and direction are confirmed by the model. The model also predicts that the patterns are more directive when the soil conductivity increases, when the contact is by means of a short skip, or when the whip curves back from the normal at high speeds. Low angle DX work is less sensitive to ground-plane orientation. Large variations from the patterns could arise from field distortions produced by nearby objects, poor electrical contact over various parts of the car body, and a bumper mount instead of a deck mount. A tilted ground plane instead of a horizontal ground plane would be a more accurate model in this latter case. The net effect would reduce the fields over the ground plane and increase the fields in the opposing quadrant.

In addition to the references listed, helpful ideas are gratefully acknowledged from two other sources: first, from conversations with K8MBV and a number of other mobile hams, and second, from the pleasant and informative hours spent in assembling, testing, and operating mobile equipment with W A4KQO.

1  King, Theory of Linear Antennas, University Press, Cambridge, Massachusetts, 1956, p. 395, 421, 687.

2  Hills, "The Ground Beneath Us," R.S.G.B. Bulletin, June 1966, p. 375.

3  Schelkunoff and Friis, Chapter Seven, Antennas/Theory and Practice, John Wiley and Sons, Inc., New York. 1952.

4  Chapter Two, The A.R.R.L. Antenna Book.

Posted November 25, 2020
(updated from original post on 12/6/2013)