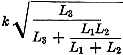Magnetostriction Devices and Mechanical Filters for Radio Frequencies
July 1953 QST

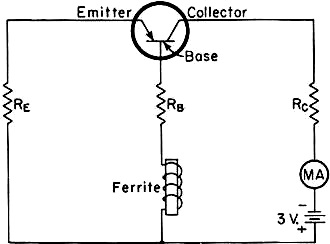
This is Part II of a 3-part series of articles on magnetostriction devices. At audio and low IF frequencies, the use of ferrite elements to construct relatively high-Q resonant circuits for filtering was a big deal in the middle of the last century. Although not presented in this article, design formulas and tables were published to implement the familiar Butterworth, constant-k, Chebyshev, Gaussian, and other types. Tuning, particularly for higher order filters, could be a chore since it involved a cut--and-try method on the ferrite rods. However, that is what was available in the day, and it evidently worked well enough to be worth the trouble for desired selectivity.

Magnetostriction Devices and Mechanical Filters for Radio Frequencies

Part II† - Filter Applications (see Part I)

By Walter Van B. Roberts,* W2CHO

In the second part of this article, some applications of mechanical resonators are discussed and a general description is given of a mechanical filter suitable for intermediate frequencies.

Some Uses for Single Mechanical Resonators

The use of a ferrite resonator as a high-Q tank circuit for an oscillator was discussed in the preceding article. An oscillator using a transistor instead of a tube, and requiring only two or three flashlight cells at negligible current drain, makes a compact portable source of known-frequency oscillations of a few hundred kilocycles or less. The frequency decreases less than 0.002 per cent per degree Fahrenheit increase of temperature. A circuit is shown in Fig. 13. Harmonics useful for checking receiver calibration can be heard, at least to 30 Mc., by directly connecting the emitter to the receiver antenna terminal (single-wire connection only).

It has been noted that the association of a ferrite resonator with a coil has the same effect as inserting, in series with the coil, a high-Q parallel-tuned circuit. The impedance of this circuit at resonance is k²Q times the coil reactance, where k is the coefficient of coupling between the coil and the resonator and Q is the mechanical Q of the resonator. Thus if, for example, k = 0.05 and Q = 2000, the resonator effectively inserts in the coil a resistance five times as great as its own reactance. Even if k is very small, a noticeable effect is produced. One application of this effect is illustrated in Fig. 14, which shows an i.f. transformer in a receiver equipped with a Magic Eye tuning indicator. A small ferrite ring, permanently biased as previously described, is slipped over the lead to a coil, and tuned to resonate in the radial mode at the center of the i.f. passband. The coupling to the entire tuned circuit is very small because the main part of the coil is not associated with the ring at all, but at resonance the ring inserts about one ohm in series with the coil and this is enough to cause a flick in the Magic Eye, and thus indicate correct tuning. Such an indicator would be useful in a high-fidelity receiver where the shadow of the eye does not change noticeably over a considerable range of tuning.

Perhaps the simplest use of a single ferrite resonator in a filter is to substitute the resonator for the middle circuit of a three-circuit filter, as shown in Fig. 15. The only difficulty here is the necessity for eliminating any appreciable direct coupling between coils by way of the ferrite resonator, which acts as a core common to the two coils. This is done by using a resonator several half waves long and putting a copper tube over the middle part, as shown by the dotted lines. This tube is grounded to ordinary shielding between circuits. The longer the tube and the smaller its diameter, the more effective it is, but it is made very long the filter band will have to be narrow. This is because the bandwidth varies with the coefficients of coupling between the resonator and the tuned circuits and these coefficients vary inversely with the square root of the number of half waves in the resonator. For example, if a coefficient of 6 per cent is available between a half-wave resonator and its coil, then if we use a four-half-waves-long resonator with a coil on only the end half wave, the coupling between the coil and whole resonator will be only 3 per cent and the bandwidth about 4.2 per cent. The band could easily be made as small as desired by using a very long resonator or by coupling the coils more loosely to its ends, except for the fact that the Q of the coils must be approximately equal to the reciprocal of the bandwidth expressed as a fraction, and this puts a lower limit to bandwidth. For example, if the best Q available is 200, then the narrowest band obtainable will be about 1/2 per cent. Fortunately, the range of about 1/2 to 4 per cent bandwidth is sufficient for many purposes.

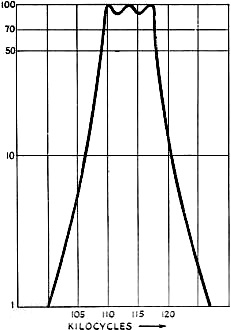
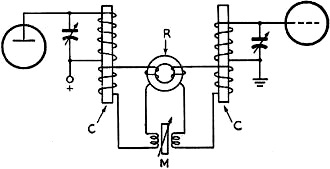
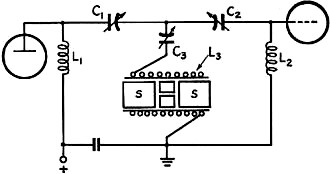
The theoretical relations between bandwidth. coefficients of coupling, and coil Qs to produce a desired transmission characteristic will be taken up later, but in practice a filter of the sort shown in Fig. 15 can most easily be tuned up by cut-and-try, the couplings, tunings and Qs being varied until a satisfactory filter curve is obtained. As an example, Fig. 16 shows the measured curve of output voltage of a filter employing a torsion ferrite 1/4 inch in diameter and three half waves long, and adjusted to give a 1.3 db. peak-to-valley ratio.

Another way to eliminate direct coupling between the circuits of a filter using a single ferrite resonator is to buck it out by means of an equal but opposite mutual inductance. This method permits using resonators which are not adapted to the shielding described above. As an example, Fig. 17 shows a ferrite ring resonator and a bucking mutual inductance M which call be adjusted by moving a core or by varying the separation between coils. In this figure R represents a radial-type ferrite resonator, and as it is not practical to wind many turns on such a torus, a few turns only are used in a link circuit coupled to the tuned circuit by a core C which is preferably composed of a nonmagnetostrictive ferrite that gives the coils a high Q. When M is adjusted for accurate balance, the performance is similar to that of Fig. 16, but by a slight unbalance the cut-off can be made steeper on one side of the passband or the other.

It is possible to use another resonator, tuned to a different frequency, to act as the bucking mutual and thus obtain a lattice filter with four-circuit performance. In fact, it is easy to construct a lattice filter with any number of resonators, but in practice the adjustments of such a filter are so complicated that for more than one resonator it is better to use the cascade type of filter to be described later.

Before leaving the subject of filters employing a single ferrite resonator, one more might be mentioned because it provides rejection points on each side of the passband. Fig. 18 shows the arrangement used in an experimental circuit giving nearly flat response over a band of 6.8 kc. at 455 kc., with rejection points 13.6 kc. apart and about 40 db. down.

In this filter a permanently-magnetized ring of ferrite is used in the torsional mode, its axial length being ground to resonate at 455 kc. This is placed inside a close-fitting coil form on which L₃ is wound, and is flanked by slugs S of inert ferrite which increase the coupling between the resonator and coil L₃. By reference to the equivalent circuit of Fig. 5 it can be seen that this is a filter of the "m-derived" type. It can be systematically tuned as follows: with C₁ and C₂ detuned, there is a sharp response at the frequency of the ferrite. With the input set to this frequency, a jumper is connected between the junction of the three condensers and ground, then circuits C₁L₁ and C₂L₂ are peaked up. (They tune substantially independently since they are coupled only by the small inductance of the jumper.) Next, the jumper is removed and C₃ adjusted until the rejection points are properly located on either side of the passband. The spacing between rejection points, as a fraction of the midband frequency, is the same as the coefficient of coupling (k) between the resonator and L₃. The bandwidth is

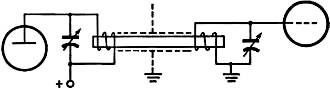
again as a fraction of midband frequency. Thus, if all three coils are alike, the band is 0.82 k. Note that the ratio of spacing between rejection points to spacing between cut-off frequencies depends only on the inductances. Flatness of transmission in the passband is obtained by adjusting the Qs of coils L₁ and L₂. The Q of coil L₃, however, should be made as high as possible by using large-size Litz wire.

The Use of Ferrites in Multielement Filters

The simplest sort of multielement electrical filter is a chain of coupled circuits as shown in Fig. 19, all circuits being tuned alike.

In this figure the ks represent the coefficients of coupling between adjacent circuits, and as explained before, the coefficient of coupling between any pair of circuits is equal to the fractional difference in frequency between the two response peaks that would be observed if the same two like-tuned, high-Q circuits were used as a two-circuit filter, like an ordinary double-tuned i.f. transformer. In other words, if we want to make k₂₃ = 0.03, for example, we would remove circuits 2 and 3 and use them as an i.f. transformer, increasing the coupling until the transmission shows twin peaks separated by 0.03 fractional (or 3 per cent) in frequency. The ds represent the dampings of the circuits, and in what follows, d is defined as 1/Q for each circuit.

Now, any combination of ks and ds will result in some sort of frequency selective transmission or filter characteristic, but the ks and ds must be chosen in accordance with appropriate equations to produce particular types of filters. Let us start by supposing that the dampings are so small as to be negligible, except those of the end circuits. Also let the desired fractional bandwidth be B. Then if we make the first and last coefficients of coupling each 0.707B and the other couplings each 0.5B while the damping of each end circuit is made equal to B, the result is what may be called a simple Campbell filter. The only trouble with this filter is that it has "ripples" toward the edges of the passband, although the transmission is quite flat around midband. However, if there are not too many circuits in the filter, the ripples near the edges of the band can be reduced, at the cost of introducing some ripple at midband, by reducing the dampings somewhat from the value given above. Very satisfactory characteristics can be obtained in this manner up to 5 or 6 circuits, but as the number of circuits is increased, the ripple gets worse.

In another type of filter called the Tchybescheff, the ks and ds are so chosen that ripples occur all through the passband, but the peaks are all equal and the valleys are all equal and the peak-to-valley ratio can be made as small as desired by suitable choice of the ks and ds. It might well be asked why then not design the filter for zero ripple? This, in fact, is easily done, and formulas for doing so are given by Dishal¹ both for filters with coupling and damping values symmetrical about the center of the chain of circuits, and for filters with damping at one end only. However, such "maximally flat" filters do not cut off nearly so sharply outside the band as do filters which have a little ripple in the band. There is a very great improvement in cut-off when even the slightest trace of ripple is permitted, so that for any ordinary purposes it is desirable to design for the maximum amount of ripple that can be tolerated. The calculation of the ks and ds to give any chosen amount of ripple with any desired number of circuits can be carried out as described in an earlier Dishal article.²

The foregoing circuit theory can now be transferred without alteration to mechanical filters by substituting ferrite resonators for the next-to-end circuits and metal resonators for the circuits in between. The couplings between end circuits and ferrite resonators now become coefficients of magnetostrictive coupling, and mechanical couplings between mechanical resonators replace the electrical couplings of Fig. 19. The resulting filter is then as shown more or less pictorially by Fig. 20.

In this arrangement the end circuits are still electrical but Circuits 2 and 6 have been replaced by ferrite torsion resonators, the couplings between the end circuits and the ferrites still being called k₁₂ and k₆₇. The middle resonators which replace circuits 3, 4, and 5 may be of aluminum. The resonators may each be a half wave long, and the coupling necks a quarter wave long, the wavelength being calculated from the velocity of propagation of torsion waves in the material used, and at mid-band frequency. The coefficient of coupling between similar torsion half-wave resonators is approximately 2/π times the fourth power of the ratio of the neck diameter to the resonator diameter, so that it can easily be made quite small. The process of design is, in principle:

1) Calculate the ks and ds required to produce the desired filter characteristic. For this use Dishal's formulae, or for a simple Campbell type filter use the values given above.

2) Calculate resonator and neck dimensions that will give the required coefficients of coupling.

3) Build the filter.

4)Tune it up and adjust the end circuit dampings and couplings.

It should be noted that these steps are all that are required "in principle." Actually, accurate tuning of the mechanical resonators is likely to be extremely difficult in practice, so that it is not recommended that any multiresonator filter be attempted until detailed suggestions, which will be included in a subsequent article, have been carefully considered. The preceding discussion is intended only as an indication of the general nature of a mechanical filter and illustrated by the particular case of a torsion filter. A somewhat different approach to the subject, particularly the simple Campbell type filter, has been described in the RCA Review.³

[The third part of this article, to appear in a subsequent issue, will describe the construction of mechanical filters for both phone and c.w., and the method of adjustment. - Editor]

† Part I of this article appeared in June, '53, QST.

1 Dishal, "Alignment and Adjustment of Synchronously Tuned Multiple-Resonant-Circuit Filters," Proc. I.R.E., November, 1951.

2 Dishal, "Design of Dissipative Band-Pass Filters," Proc. I.R.E., September, 1949.

3 Roberts and Burns, .. Mechanical Filters for Radio Frequencies," RCA Review, September, 1949.

Posted March 22, 2022
(updated from original post on 5/16/2016)