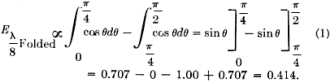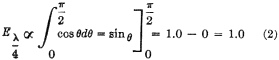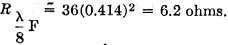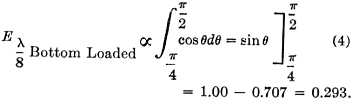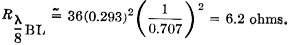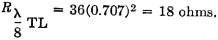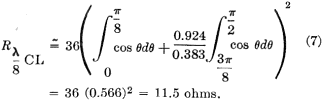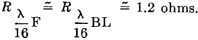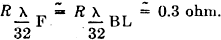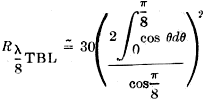Folded and Loaded Antennas
April 1953 QST Article

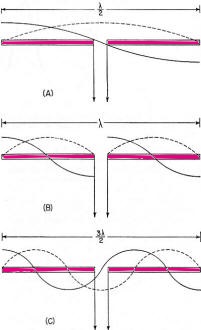
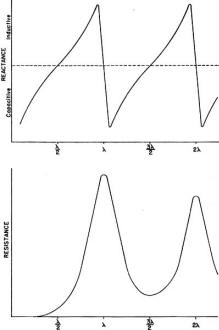
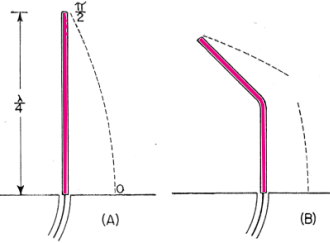
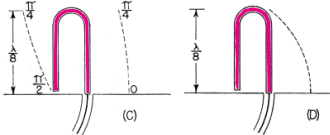
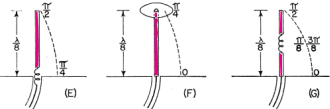
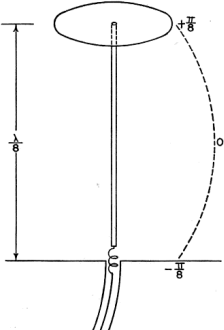
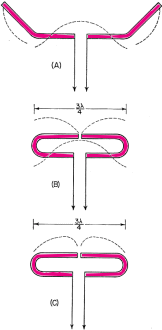
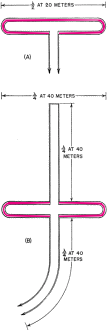
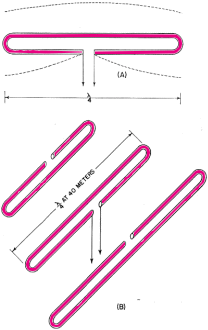
Here is a fairly major treatise on folded and loaded antennas that appeared in a 1953 issue of QST magazine, with "Suggestions for Mobile and Restricted-Space Radiators." It is not for the faint of heart or anyone with mathphobia. Integral calculus is part of the presentation, although an understanding of calculus is not required to get the gist of the article. Equations for calculating the antenna configuration radiation resistances are given for the 3λ/4-wave folded dipole, the λ/8-wave folded monopole, the bottom-, center- and top-loaded λ/8-wave monopole, the bottom-loaded λ/16-wave monopole, and the λ/4-wave monopole folded twice, to name a few.

Folded and Loaded Antennas

Suggestions for Mobile and Restricted-Space Radiators

By William B. Wrigley,* W4UCW

Using a simplified method of calculation, the author develops values for the radiation resistance of various folded and loaded forms of short antennas. Several interesting possibilities for small radiating systems are discussed.

While we are all quite familiar with the half-wave folded dipole, its radiation pat­tern, input or radiation impedance, and application to amateur installations, it seems that there are many more folded configurations which are not well known and which may prove quite surprising in their usefulness. Most of us are also reasonably familiar with the basic methods of loading mobile antennas, but we may be surprised at what a few simple calculations can tell us about the effects of various methods of loading.

First let us consider the basic half-wave thin dipole¹ with a theoretical balanced center-feed impedance of about 72 ohms. Fig. 1A shows such an antenna with its current distribution (dashed line) and charge distribution (solid line). While these distributions are not exactly sinusoidal as shown, the assumption that they are so introduces negligible error in impedance and field-pattern calculations, and at the same time reduces these calculations from formidable complexity to fairly simple operations. Now Fig. 1B shows what happens if we attempt to operate this antenna at the second harmonic. We now have a condition of antiresonance. The input resistance is much higher and the reactance variation with frequency is much greater than in the original resonant case at the fundamental frequency. Fig. 10 shows the current distribution at the third harmonic, where we once again have a reasonably broad resonant condition. Fig. 2 shows qualitatively this same information as resistance and reactance plotted against antenna length in wavelengths.

We might conclude from all this that, at least in the symmetrical case, an antenna will be rea­sonably broad-band only at frequencies where the length is an odd number of half-wavelengths or such that the feed point is at a current maximum.

Why can we not simply move the feed point to a current maximum in the second-harmonic case of Fig. 1B? We can, in fact, but then things change somewhat since the now-continuous center cannot support a discontinuity in charge. So we get distributions as shown in Fig.  3A, somewhat unbalanced, as would be expected. Since the charge polarity is now the same at both ends, however, we can fold the left current loop over the driven loop as shown in Fig. 3B and obtain the familiar folded dipole of Fig. 3C, which is, of course, quite symmetrical. The impedance of this folded arrangement can be found by considering it as merely an impedance transformer between the feeder line and free space. The far-field intensity normal to the axis of the antenna is proportional to the total current added up along both wires and, since we now have exactly double the current producing the far field, as compared to that in either wire alone (in particular the one being fed), we must have double the far-field pattern strength. However, the transmission line furnishes power that is exactly the same as in a simple dipole, hence the input or radiation resistance must be directly proportional to the square of the total far-field intensity as compared to that of the fed wire only (W = E² / R). In this case 2² = 4 and 4 x 72 is 288 ohms, which is the approximate theoretical radiation resistance of a thin folded half-wave dipole. It is well known that the reactance-frequency variation of the antenna is, in this particular case, partially cancelled out by the opposite variation of the two transmission line stubs in series seen from the feed point such that the folded dipole has, in fact, broader bandwidth than the single thin dipole.

Other Folded and Loaded Systems

Since this folding operation has proved so attractive, let us now investigate the possibility of folding the configuration of Fig. 1A. Because of the mobile antenna application we shall consider half the antenna of Fig. 1A against a ground plane and fed with a coaxial cable as shown in Fig. 4A. We can fold the antenna as in Fig. 4B and obtain the eighth-wave folded monopole of Fig. 4C? Since the opposite ends of the original dipole were at opposite charge polarity (Fig. 1A), we must leave these ends unconnected upon folding; or, in the ground plane case, the folded-over section must not be allowed to contact the ground plane. For radiation purposes, the current in the folded section is opposite in direction to that of the unfolded half and one must be subtracted from the other, resulting in the radiation current distribution shown in Fig. 4D.

Now in the folded dipole case we found the impedance by adding (mathematically integrating) the current distribution along the wire to obtain a figure proportional to far-field strength.

Actually, these figures of proportionality are only valid comparisons of two antennas if the far-field patterns or current distributions are identical. However, in all the cases we shall consider here, there will be only one combined radiating current loop and hence only one far-field pattern lobe. These lobes will not be exactly the same shape, but to assume them so is a reasonable approximation as evidenced by the fact that the far-field radiation pattern of a half-wave dipole with sinusoidal current distribution is only slightly more directive (78 degrees between half-power points) than that of a minutely short dipole with uniform current distribution (90 degrees between half-power points).

As shown by the calculations in the Appendix, the approximate radiation impedance of the folded eighth-wave monopole of Fig. 4D is 6.2 ohms. A similar analysis of a bottom-loaded eighth-wave monopole, Fig. 4E, shows that its radiation resistance also is 6.2 ohms, which is the same as for the folded case! This identity holds for a quarter-wave monopole which is folded into any even number of elements as compared to a bottom-loaded single element of the same actual height.

Fig. 4F shows the current distribution of a top-loaded eighth-wave monopole.³ The approximate radiation resistance, as shown in the Appendix, is 18 ohms. For the center-loaded eighth-wave monopole of Fig. 4G the approximate method of calculation still applies and leads to a theoretical radiation resistance of 11.5 ohms.

Folded Mobiles

Fig. 4D could be interpreted as a 20-meter mobile antenna made up of two adjacent eight-foot whips. One significant advantage of this arrangement is that there is no loading-coil loss to contend with. A further advantage is in the realization that a shorted stub of appropriate length (λ/4 at 20 meters) connected to the mounting point of the folded or second whip will be an open circuit at 20 meters and a closed circuit at 10 meters. At 10 meters the system becomes a quarter-wave folded monopole (half a folded dipole) with an input impedance of a little over 100 ohms, while at 20 meters, with no mechanical change, it becomes an eighth-wave folded monopole with an impedance of about 5 ohms. (Five ohms is probably closer than the theoretical 6.2 ohms since mobile quarter-wave whips look more like 30 than 36 ohms. They are not "thin.") The rather severe difference in impedance between the fundamental and second-harmonic case can be taken care of by feeding the pair of whips with another quarter-wavelength of cable at 20 meters. Being a half-wave at 10 meters, this would give a load impedance at the transmitter of somewhat over 100 ohms at 10 meters and Z_o² / 5 ohms at 20 meters, where Z_o is the characteristic impedance of the cable used. This double whip 10-20 system will be slightly more selective, however, than either of the plain folded monopoles, since the reactance deviation with frequency of the shorted stub is opposite in sign from that required to counteract the reactance deviation of the antenna.

If a 40-meter quarter-wave monopole were folded down to eight-foot height there would be four sections. The resulting impedance, which again is the same as that of a bottom-loaded sixteenth-wave monopole, is 1.2 ohms (see Appendix). An 80-meter arrangement would take eight whips and would have an impedance of approximately 0.3 ohm. However, these latter two extensions of the folding process do not immediately appear very attractive. To complete our discussion of folded and loaded monopoles we should include the radiation resistances of 40- and 80-meter loaded antennas. Table I shows all of these figures calculated by the far-field factor method and based on a nominal quarter-wave monopole impedance of 30 ohms, more realistic than the theoretical "thin" monopole value of 36 ohms.

It is interesting to investigate the impedances of short monopoles with optimum current distributions. This requires loading at both top and bottom so as to center the current loop on the antenna as shown in Fig. 5. The values of radiation resistance for 40 and 80 meters are also included in Table I.

A top- and bottom-loaded (current loop centered) 10-meter quarter-wave monopole has the very attractive impedance of 120 ohms, calculated by this method. The ground current losses in it would be considerably less than the losses in the unloaded case for the same radiated power.

Comparisons

We can now draw some very definite conclusions regarding the merits of various loading schemes. Since the principal loss in a vertical radiator (outside of the loading-coil loss) is due to ground currents, the efficiency rapidly decreases with decreasing radiation resistance. For constant radiated power, the current must be greater for smaller values of radiation resistance. Greater current means greater loss and consequent reduction in efficiency; therefore, the power loss in a center-loaded eighth-wave monopole is more than that of a top-loaded equivalent antenna and the loss in the bottom-loaded case is more than that of the center-loaded case. A combination of both top and bottom loading, however, gives a radiation impedance which in some cases reduces the loss to an exceptionally low value compared to that of the bottom-only loaded, folded, or unloaded case. Sufficient top loading is usually impractical, however, particularly in the case of very short monopoles.

The main conclusion we can draw from all these calculations is that short antennas (monopoles less than one-tenth wavelength) have uncomfortably low radiation resistances and practically nothing can be done to improve their efficiencies to a reasonable value, except possibly by using a multiwire system to raise the impedance as described earlier. On the other hand, the efficiencies of longer (quarter- or eighth-wave) monopoles may be increased considerably by proper loading, or folding. A practical example is the 160-meter folded eighth-wavelength three-wire monopole shown in Fig. 6B. Adding a third wire to the folded quarter-wave monopole, Fig. 6C, raises the resistance to about 300 ohms, and when this antenna is folded over as shown in Fig. 6D, the radiation resistance becomes about 50 ohms, a good match for coaxial cable. Suggested dimensions for 1850 kc. are given in the sketch.

3λ/4 Folded Dipole

Now, since we have pretty well folded and loaded Fig. 1A, let us investigate the results of folding Fig. 1C. This process and the resulting current distribution is shown in Fig. 7 where the center line represents a ground plane for the vertical analogue of the system. Calculation leads to an impedance for this three-quarter wave folded dipole of about 420 ohms. J. D. Kraus ^{5, 6} (W8JK) has measured one of these to be about 450 ohms. The new 21-Mc. band makes this arrangement quite useful as can be seen in the following scheme:

Suppose we start with the 20-meter folded dipole of Fig. 8A and open-circuit the top dipole opposite the feed point. We now have a quarter-wave folded dipole at 40 meters, the vertical analogue of which we have already discussed. The impedance of this dipole at 40 meters should be about 12 ohms. A λ/4 length of Twin-Lead at 40 meters would then transform this to Z_o²/12 at the transmitter. A shorted λ/4 stub connected to the open ends of the dipole as shown in Fig. 8B would provide an open circuit at 40 meters, a short circuit (λ/2) at 20 meters, and open again (3λ/4) at 15 meters. At 20 meters we have our original half-wave folded dipole and at 15 meters we have our 3λ/4 folded dipole. In this last case the now 3λ/4 feed line transforms the impedance to Z_o²/420 at the transmitter. Of course, the shorted stub may be folded up in some convenient way so as not to consume all the space indicated in Fig.8B.

The radiation patterns of the antenna are practically identical at all three frequencies.

Other Possibilities

No doubt there are many more folded arrangements which may prove attractive, such as the possibility of a 40-meter close-spaced beam made up of quarter-wave folded dipoles. Now, due to the coupling of the parasitic elements, the impedance of the driven element would be considerably lower than the 10 to 12 ohms of a folded quarter-wave dipole in free space. This may be raised to a more reasonable value, however, by feeding at the current node (voltage feed) rather than at the current loop.² The driven element would then look just like a 20-meter folded half-wave dipole, but the current distribution would be as shown in Fig. 9A and the entire array would look something like Fig. 9B. A T-match or a "Q"-section at the feed point may provide an even better driving-point impedance. The approximate over-all lengths of the elements, before folding, may be determined from the curves for 20-meter elements given in The Radio Amateur's Handbook or in the ARRL Antenna Book, simply by dividing the frequency scale in half and doubling the length scale.

With some compromise in element spacing this array may even be operated as a combination 40-20-15 beam by the use of small lumped networks in the parasitic elements in place of the rotationally cumbersome stubs of Fig. 8B. In case you would like to try this latter arrangement, Fig. 10A shows the impedance vs. frequency characteristic required and Fig. 10B shows a suitable network to accomplish this. The parameter K allows for variation in the over-all impedance level, but should be chosen so as to make C₁ a conveniently small capacitor and include the capacity between the two ends of the element. Since harmonic antennas are not, in general, exact multiples of length, all the network elements may require some adjustment after final assembly to approach resonance on all three bands.

Fig. 10 - Impedance variations in the frequency range of interest (A) and a lumped-circuit equivalent of the stub shown in Fig. 8. Component values can be calculated from the following formulas, where f is in megacycles:

C₁ = K μμfd.

C₂ = 2.4K μμfd.

L₁ 4220/Kf² μh.

L2 = 1.67 L₁ μh.

The factor K may be chosen to make the inductances and capacitances come out to convenient or constructionally-feasible values.

Appendix A

λ/8 Folded Monopole Antenna Radiation Resistance (Fig. 4C)

To find the radiation impedance of the eighth-wave folded monopole we must find the far-field figure of proportionality normal to the axis of the antenna by subtracting the integrated current of the folded-over half from the integrated current of the unfolded half. The total length is

λ/4 or π/4 radians so

= 0.707 - 0 - 1.00 +0.707 = 0.414.

This is the far-field proportionality constant whose square must be compared with that of a known antenna to give the impedance. The known standard is, of course, the thin quarter-wave monopole whose figure is

and whose theoretical input impedance is about 36 ohms.

Therefore, the approximate radiation impedance of the thin folded eighth-wave monopole is

Bottom-Loaded λ/8 Monopole Antenna Radiation Resistance (Fig. 4E)

The current distribution on a bottom-loaded eighth-wave monopole, Fig. 4E, is identical with the top half of the quarter-wave monopole which we folded over in the previous case, since the loading coil merely replaces the missing half. We can calculate the radiation resistance of the remaining half as follows:

1.00 - 0.707 = 0.293.

This far-field figure, however, concerns the impedance referred to a current maximum point and since we are feeding at the π/4 or 45-degree point we must divide by the square of the cosine of 45 degrees (constant power impedance is inversely proportional to the square of the current). So finally we get

Top-Loaded λ/8 Monopole Antenna Radiation Resistance (Fig. 4F)

The approximate radiation resistance can be calculated from the cosine integral from 0 to π/4 which gives a far-field factor of 0.707.

Center-Loaded λ/8 Monopole Antenna Radiation Resistance (Fig. 4G)

For the center-loaded case the calculation is a little more complicated. but our approximate method still applies. The far-field factor includes two additive components, the first of which comes from the bottom section of the antenna and is merely the cosine integral from 0 to π/8. The loading coil effectively replaces the missing center half of the antenna so that the current distribution along the top section is essentially the cosine curve from 3π/8 to π/2. Since the current is continuous through the coil, however, this second integral must be multiplied by the ratio of the cosines of π/8 and 3π/8. The approximate theoretical radiation resistance of a center-loaded eighth-wave monopole is then

= 36 (0.566)² = 11.5 ohms.

Bottom-Loaded λ/16 Monopole or λ/4 Monopole Folded Twice Antenna Radiation Resistance

The cosine integral is broken down into four equal parts between 0 and π/2 or 90 degrees. Two alternate parts are added and the other two are subtracted. The resulting impedance, which is the same as that of a bottom-loaded sixteenth-wavelength monopole, is

λ/32 Monopole Antenna Radiation Resistance

(Eight integrals)

Top- and Bottom-Loaded λ/8 Monopole Antenna Radiation Resistance (Fig. 5)

In this case the far-field factor is twice the cosine integral from 0 to π/8. In calculating the impedance, however, we must divide by the square of the cosine of π/8 or 22.5 degrees, since we are feeding at a point 22.5 degrees from the current loop. This is similar to the case considered in equation (5). Therefore,

= 30 (0.830)² = 21 ohms.

3λ/4 Folded Dipole (Fig. 7C)

The far-field factor for this case is found by calculating the difference between the cosine integral from 0 to 3π/4 and the integral from 3π/4 to 3π/2. This figure is 2.414 and from this the impedance of the folded 3/4-wave dipole comes out to be about 420 ohms.

* Asst. Prof. Research, Georgia Institute of Technology.

1 Editor's Note: As some readers may not he familiar with the terms used here, the following may be helpful:

A "thin" antenna is one having a very large ratio of length to conductor diameter, approaching infinitely-small diameter; practically, a wire antenna at low frequencies is "thin" but a 10-meter beam element is fairly "thick." The thickness affects the resonant length, radiation resistance, and sharpness of tuning.

"Antiresonance" is the same as parallel resonance; in the antenna case, it is the condition that exists when a resonant antenna is viewed at a voltage loop.

"Charge" and "charge distribution" are equivalent to "voltage" and "voltage distribution."

The" far field" is the radiation field at a large distance from the antenna - so far that the waves may be considered to be plane waves, and, of course, far beyond the region where the induction field is of any consequence.

A "monopole" is one-half of a dipole; e.g., a grounded antenna or one in which a ground plane is substituted for actual ground.

2 Lindenblad, "Television Transmitting Antenna for Empire State Building." RCA Review, 3, p. 400, April, 1939.

3 Terman, Radio Enoineers' Handbook, McGraw-Hill Book Co., Inc., New York, 1943, par. 11, sec. 11.

4 Jordan, Electromagnetic Waves and Radiating Systems, Prentice Hall, Inc., New York, 1950, pp. 510-517.

5 Kraus, Antennas, McGraw-Hill Book Co., Inc., New York, 1950; particularly Chapter 5 and par. 13 of Chapter 14.

6 Kraus, "Multiwire Dipole Antennas," Electronics, 13, pp. 26-27, Jan., 1940.

Posted April 19, 2016