Bandwidth Requirements for Pulse-Type Transmissions |
|
In 1945, when this article was published in QST magazine, radar was still in its infancy. Engineers were already aware of the need to shape pulse waveforms from experience with CW keying and the need to mitigate the effects of "chirping." A perfectly rectangular pulse in the time domain, as we learned in our signals and systems courses, creates a sin (x)/x response in the frequency domain. The Fourier transform shows that a perfectly square pulse in the time domain is the summation of an infinite number of odd harmonics of the fundamental (1st harmonic). The first few harmonics are audible to the CW copier as higher frequency "chirps." To reduce the annoyance (and wasted transmitted energy), time constants were added to the leading and trailing edges of the waveform to remove the higher frequencies, while leaving the pulse shape sufficiently rectangular to achieve its goal. The same type issue applies to radar pulses. Bandwidth Requirements for Pulse-Type Transmissions A Discussions of Wave Shape as a Guide in Frequency Allocations By W. W. Hansen (Research Engineer, Sperry Gyroscope Co., Inc., Garden City, N.Y.) IN MAKING suggestions as to suitable allocations of wave bands in the microwave region for the future, due caution should be exercised in considering any proposed system which uses grossly more bandwidth than the minimum required by the information communicated. It may be that wave bands can be allotted more liberally in the microwave region than in the long-wave region, simply because there is so much band space available that it is difficult to see at present how all of it can be used. Nevertheless, the history of the spark transmitter suggests that caution is in order; at least serious thought should be given before systems using excessive spectrum space are permitted. It is the object of this article to present some information relative to one family of such systems and to make some suggestions as to possible regulations which might usefully be imposed on such types of transmissions. Modulating Systems Pulse technique in which the carrier is broken up at regular intervals before modulation probably is one of the most important radio developments since the beginning of the war. lts possible applications still are far from being fully explored. While it is apparent that greater band-widths are required for transmissions of this type, certain advantages may be gained if it is possible to operate under conditions where band-width is not of too great importance. This, of course, points to applications which make use of much higher frequencies than those heretofore employed by amateurs. Among the advantages claimed for pulse-type transmissions are a considerable improvement, in signal-to-noise ratio and the simplification of equipment. Since there may be ways in which this technique can be used to advantage in amateur work of the future, this discussion of pulse shape in relation to spectrum economy should be of unusual interest. The type of systems we have in mind perhaps may be illustrated by means of an example. Suppose the information we wish to transmit has frequencies up to 10 kc. Then assume that we choose some higher frequency, say 20 kc. as a "subcarrier." The transmitter then is turned on and off at a 20-kc. rate. This is called discontinuous modulation. When the signal input voltage is zero, the transmitter is on half the time and off half the time. In other words, the microwave modulation envelope is a 20-kc. square wave with equal" on" and "off" periods. Then to modulate upward, one increases the time the transmitter is on and decreases the time it is off, 100 percent modulation occurring when the transmitter is on continuously. To modulate downward, one decreases the fraction of the time the transmitter is on. More generally, the unmodulated condition can correspond to the transmitter being on less (or more) than half the time. For example, one microsecond pulses at a rate of 1000 pulses per second might correspond to no modulation and two-microsecond pulses to 100 percent upward modulation. Another possible system is one having all pulses of the same duration but varying in the number per second in accordance with the information-bearing modulation. Still another method would be to vary the phase of the pulses in accordance with the signal modulation. The advantage of such systems is that they will work with power sources that cannot be modulated linearly in a continuous manner. Another point is that a great deal of suitable technique is available as a result of war-inspired research. Incidentally, one of these systems was used in the early microwave link across the English channel developed by I.T.T. about ten years ago. Pulse Shapes Let us now inquire into the frequency spectrum required by such a system. Fundamental to the problem is the frequency spectrum corresponding to a single typical pulse. This depends, of course, upon the shape of the pulse. We shall give results for two pulse shapes which, it would seem, constitute a sort of upper and lower boundary for pulses which may be realized in practice. Consider first, then, a simple flat-topped pulse of duration to.
The frequency spectrum corresponding to this pulse is Consider next a pulse in the form Actual pulse forms which may be used will fall between the above two limits. The frequency spectrum cannot fall off as slowly as that first considered, because the start and finish of the pulse cannot be perfectly abrupt, as assumed. On the other hand, a pulse as smooth as the Gauss-error type discussed above is not likely in practice.
Fig. 1- Graph of modulation envelope with pulse. type transmission. Pulse Modulation Next, what happens if a series of pulses is used to modulate a carrier? If they are evenly spaced and of uniform intensity, as we shall assume for a moment, then the frequency spectrum is as illustrated qualitatively in the graph of Fig. 1 which is drawn for the Gauss-error-curve type of pulse. Here the origin corresponds to the carrier fre-quency and the various peaks are spaced f1 apart, where f1 is the subcarrier frequency. The dotted line, which is the envelope, has the same shape as the spectrum of a single pulse. Strictly speaking, the various peaks, which have been drawn with a small but finite width, should be infinitely narrow and infinitely high but with a finite area corre-sponding to the dotted-envelope curve. If, finally, we vary the height of the various pulses according to some signal voltage, each peak spreads out to a width corresponding to the frequencies contained in the signal voltage. We will call the highest frequency contained in the signal voltage f2. Band-Width Requirements Actually, the modulation is not done by varying the height, but the width or the frequency or the phase of the pulses. This complicates the analysis too much for discussion here but one point, and it is the essential one, remains unchanged. Namely, the frequency spectrum follows roughly the spectrum corresponding to a single pulse; or, stated more exactly, the envelope of the frequency spectrum follows the spectrum of a single pulse. From the above we see that the amount of spectrum used is of the order of 1/to, whereas one could transmit the information with a band 2f2 (or f2, if a single-sideband transmission were used). Thus, one uses roughly 1/f2to times as much spectrum as need be. How big is this factor? If one makes the subcarrier, f, only slightly greater than f2 and makes to = 1/2f1 (i.e, uses a square wave as an unmodulated signal), then the factor 1/f2to is not significantly different from two, and there is little, if any, waste of frequency spectrum. (This statement will be subject to some qualification later.) If, on the other hand, for some reason to is made quite small, say, for example 10-6 seconds, while f2 is, say 104 cycles per second, then one uses about 100 times more spectrum than necessary. In some cases some of this waste can be recovered while still using the same general scheme of modulation. For example, a number of stations can be assigned the same carrier frequency provided they are assigned different subcarriers. Then a band-pass filter in the receiver will separate the signals from various transmitters. Interference Capability In the above we have considered the band used as that between the 71-percent points. But, although most of the energy usually will lie in this region, this is not the whole story when it comes to interference. What we want to know is over how wide a band will there be enough energy to cause interference. Plainly, this is a question which is difficult to answer quantitatively. Besides the obvious arbitrariness involved in deciding how much energy will cause interference, etc., there is the very important matter of pulse shape. Indeed, as the calculations above show, this is probably the most important single factor. Thus, whereas a smooth pulse of Gauss-error form of about one microsecond duration will cause no appreciable interference outside a band a megacycle or two wide, a flat-topped pulse with perfectly square corners would cause interference that would probably be called important over 20 Mc. or more. What conclusions are to be drawn from the above? There follow certain suggestions and opinions of the author which may form a partial answer to this question. If the subcarrier frequency is not much higher than the highest information frequency and the average pulse length not much shorter than a half cycle of the subcarrier frequency, there is no essential waste of frequency spectrum. But to avoid interference because of tails of the frequency spectrum, the regulations should call for some means of reducing the harmonics of the sub-carrier frequency; in other words, rounding the corners of the pulses. Some ideas on this point will be suggested later. If the pulse length is markedly short compared to the reciprocal of the highest information frequency, necessarily there is a waste of frequency spectrum, unless the purpose is multiplex transmission, and it should be considered carefully whether this is warranted. For example, with one microsecond pulses, there would be room for rather less than 300 stations between 9 cm. and 10 cm. In the author's opinion, probably there are enough available frequencies to allow such waste, provided certain conditions are imposed. Use of Filters Some means must be provided to round the corners of the transmitted pulses, as mentioned before, so avoiding an additional wastage of frequency spectrum by a factor which may amount to ten or more. Rounding the corners of the d.c. voltage pulse will not be permissible in some cases, since many of the tubes on which this system will be used have a strong tendency toward frequency modulation. Besides, this defeats the main purpose of discontinuous modulation. The simplest and best method would appear to be the requirement of a filter in the antenna line. This appears to be a thoroughly practical scheme. For example, with one-microsecond pulses one could use one or more resonators with bandwidths of about one megacycle between the transmitter and the antenna. How many stages of filter should be required is a question to be answered by the conditions prevailing in each case. The author would suggest that two would be sufficient in most cases. Conclusions Use of the modulation system suggested should be confined to certain restricted bands, leaving other bands where more normal systems will be free from what might perhaps be styled "super monkey chatter." This should present no difficulty since advocates of this system will no doubt claim that it does not cause undue interference. They should, therefore, be quite pleased to have various interference-free regions of the spectrum to themselves. Finally, the author would like to add that almost all the above applies to pulsed radar sys-tems, except that in this case the use of short pulses is often a real necessity, not a matter of real or fancied convenience. In the author's opinion much trouble would be avoided if all pulse systems were put in a segregated band, and if output filters to cut off the frequency tails were required. As to the first, there is certainly no reason to burden television and other communications services using continuous modulation with the difficult problem of putting up with pulse interference caused by discontinuous modulation. As to the second, such filters need not interfere with the performance of a system. They are cheap and easy to apply, and will greatly reduce interference potentialities.
Posted January 22, 2021 |
|
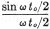and the distance
between 71-percent points on a frequency scale is easily found to be 0.88/to.
While the distance between 71-percent points is a good measure of the frequency
interval containing most of the energy, it should be noted that the above function
drops off rather slowly with ω so that considerable intensity exists at high
values of ω. Specifically the envelope of the function is 1/
the numerical factor being so chosen that the time
between 71-percent points is to. Then one finds the frequency spectrum to be
of the form 
and from this we find the separation of the 71-percent
points on frequency to be 0.44/to. Also, at a frequency ten times
the frequency at the 71-percent point the function is down by about 15 powers
of ten or 300 decibels in power. This is to be compared with 26 decibels for
the square pulse. 