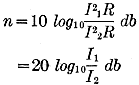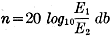|
August 1931 QST
 Table of Contents Table of Contents
Wax nostalgic about and learn from the history of early electronics. See articles
from
QST, published December 1915 - present (visit ARRL
for info). All copyrights hereby acknowledged.
|
There is no such thing as too many
good articles about the decibel, and this "What Is This Thing Called Decibel?"
piece from a 1931 issue of QST magazine is definitely a good read.
Decibels are a very convenient method for calculating changes in power, voltage,
and current levels due to it being based on logarithms, thereby changing
multiplication and division operations into addition and subtraction operations,
respectively. Once explained,
some initial fear felt by newcomers is assuaged. Thereafter, the most difficult
aspect of decibels is mathematically converting between ratios and decibels. In delving into some of the history of the usage
of the decibel, co-author McLaughlin mentions the "R" system (Readability) of
describing signal strength, as opposed to the modern "S" units - an interesting
bit of historical trivia. Keeping in mind that this was written in 1931, it is not too surprising
to read the author mention the somewhat recent transition from communications over
copper wires to "radio circuits through space."
What Is This Thing Called Decibel?
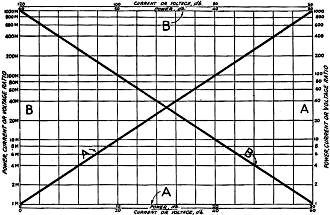
Fig. 1 - The Graphical "Gain" Table
Coordinates marked "A" are used for the "A" curve and those marked "B" go with
the "B" curve. Instructions for making up the curves and suggestions for their use
are given in the text.
For Figure 1, "Gain"
An Amateur View of the Transmission Unit
By James L. McLaughlin * and James J. Lamb, Technical Editor
Anyone who makes a practice of at least skimming through the technical literature
of radio cannot have escaped noticing the increasingly frequent occurrence of "db"
peppering its pages. Once pretty much restricted to papers and articles involving
only telephony and broadcasting, it is now quite usual to find "db" popping up in
technical stories which have little or no connection with wire telephony and often
having but incidental relationship with telephony of any kind. Comparisons of the
relative strengths of c.w. signals and the directivity of antennas, for instance,
are surprisingly satisfying and meaningful when described simply in terms of decibels.
And when something becomes satisfying and meaningful for the description of c.w.
signals and the relative merits of antennas it becomes pronto one of those things
that amateurs welcome to their circle and must needs adopt. True enough, amateurs
in considerable numbers do have a friendly working acquaintance with the db; and
its appearance in QST's pages is by this time no novelty.1 But it must
be acknowledged that an aroma of mystery and the undeserved taint of "too technical"
have become attached to the poor decibel, seriously handicapping its wholehearted
adoption by many who have genuine use for it as a simplification in the handling
of things radio - especially in the amateur field. Hence this little story; an attempt
to do right by our little decibel and send it on its merry way to popularity with
the ham of the species.
How The dB Came to Be
So far we have not so much as intimated what the family origin of our subject
might be. For purposes of getting acquainted this matter is, of course, of some
importance, even though we know that the origins of electrical measuring units are
soon forgotten in the process of putting them to work on practical problems. Witness
the general acceptance of the volt, the ampere, the watt, the ohm, as practical
yardsticks for our radio measurements, with never a thought to their fundamental
derivation. In fact, they have for us an almost physical reality - just as pints
and quarts have to folks in other lines of more or less scientific endeavor. And
so it is with the decibel. To hear those of the inner circle glibly bandy "db up"
and "db down" is to marvel at the facility with which we technical people can take
terms that have nothing more solid than abstract mathematical ratios as their basis
and adopt them as genuine realities. That is what we have done with everyone of
our electrical terms (who doesn't think of a 75-watter as having genuine physical
dimensions?) and that is what we cannot help but do with the decibel. For just as
the ohm is based on nothing more real than a mathematical ratio between volts and
amperes, so the decibel is based on a mathematical ratio between power values. It
differs slightly from other ratios in that it is logarithmic, which may seem discouraging
but shouldn't, and it actually has a genuine physical meaning not possessed by most
electrical units of measurement; it places power ratio and sound sensation as detected
by the ear on a common basis. We "hear logarithmically"; our ears do not detect
equal steps of loudness for equal steps in the power of sound but detect equal steps
in a scale of loudness more nearly as equal steps in a logarithmic scale of sound
power ratios. All of which may appear somewhat far-fetched and remote from the measurement
of signal strengths and of antenna efficiencies until we recollect that amateur
systems of communication invariably introduce the ear as the final piece of equipment;
and that unqualified measurements in terms of volts, amperes, watts, and such do
not fit the peculiarities of our personal listening apparatus.
When It Started
In the early development of telephony, a systematic relationship of electrical
power ratio to sound sensation soon became necessary. To the telephone engineer,
and to the radio engineer as well, sound is a commodity to be transformed and transported
from producer to consumer through a transmitting medium. In the early days of electrical
communication the medium was essentially a circuit of wire, but this has been extended
more lately to include also radio circuits through space. Be the circuit wire or
spatial, every piece of equipment in it between the source and a distant point means
either a gain or loss in power level which must be translated to terms of sound
value. Once upon a time different values in power level were simply but crudely
specified as "a little louder," "not so loud," and so on - not even so exact as
our old amateur "R" system of describing signal strength.
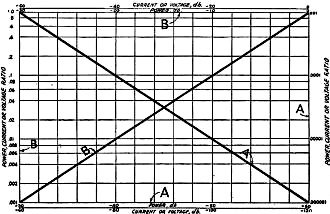
Fig. 2 - The "Loss" Table

For Figure 1, "Loss"
In search for a measuring unit for expressing more definitely different values
of power level in terms of sound value, the resourceful telephone people hit upon
the idea of the "standard cable mile." This unit of power ratio was equivalent to
the transmission loss of one mile of standard No. 19 telephone cable having a resistance
of 88 ohms per loop mile and a capacity of .054 μfd. per mile. Of course telephone
engineers could not be eternally lugging cumbersome reels of this cable around with
them, and compact artificial cables containing lumped resistance and capacity were
used as a necessary convenience.
Now the "mile" unit had two characteristics, one good and the other not so good.
The good one was that for speech the transmission loss of a "mile" quite closely
represented the smallest step on a loudness scale that the ear could detect; the
bad one was that it had a vicious frequency characteristic. It attenuated higher
frequencies more than it attenuated the lower frequencies. It was not distortionless.
This was not so serious where only" talking" tests had to be made, but when it came
to making accurate measurements at single frequencies the thing became nearly meaningless.
This was helped somewhat by adopting a standard frequency representative of speech,
this frequency being first chosen as 800 cycles and later as 1000 cycles. Of course
there was a lot more than this to the first epoch of power level measurement history,
but this abridged version will suffice to bring us to the modern era. It does indicate,
however, that the development of a completely satisfactory unit of power level measurement
is not something that might occur accidentally along about the 37th CQ on a crowded
Saturday night.
Enter the Decibel
As soon as the "mile" became so obviously unsatisfactory for the advancing art
of electrical communication, the ever ingenious telephone engineers went gunning
for a better unit which would not be greatly different in value from the old unit
at speech frequencies, but which at the same time would be distortionless and hence
more generally useful. This unit was not derived by the cut-and-try method which
brought about the "mile," but originated on a slightly higher plane. It was born
more through mathematical evolution, the process being best shown, perhaps, by a
general example.
Suppose we have a uniform signaling circuit (telephone or radio) having a length
of n miles and suppose that the power at the input end of this circuit has a value
of P1. Suppose we next measure the power at a point 1 mile from the source
and designate this power value as P2. The ratio r of the two power values
is P1/P2. Continuing the process, let us measure the power
values at successive points each 1 mile further from the source. The successive
power ratios will be found to be r2, r3, r4, etc.,
the ratio for a point n miles from the first point being rn, Very clearly,
the power ratio is an exponential function of the length of the circuit. Coincidentally,
it will be found that the sound level is directly proportional to the loop length
of the line and hence to the exponential power ratio. Now let us put this power
ratio in the form of a general equation:
P1/P2 = rn
This Logarithmic Business
Now what we are after is the value of the exponent n as derived from the ratio
of the two power values. Recalling what we may have forgotten about such things,
or digging out the old "math" book if we can't recall it, we find that this exponential
relation may be put in logarithmic form, equating the exponent to the other terms:
n = logr (P1/P2)
We are closer to the working version of the thing by this time, except for assigning
a numerical value to r in the "log to the base r" part of it. Again going back to
our school-day" math," we re-discover that there are two systems of logarithms in
general use: The Naperian system in which the base, designated e, is 2.71828; and
the Briggs, decimal, or common, system in which the base is an even 10. Both of
these systems are used for expressing logarithmic power ratios, the Naperian system
giving a basic unit called the "neper" and the decimal system giving a basic unit
called the "bel." Our decibel is a subdivision of the latter and the base 10 is
therefore the one for us. Now our logarithmic power ratio equation looks like this:
n = log10 (P1/P2) bels
Since it happens that the bel is too large a unit for practical work and since
the old" mile" unit is approximately equivalent to a unit one-tenth the size of
the bel, we divide the right-hand side of the above equation by one-tenth and obtain
the expression for logarithmic power ratio in decibels:
n = 10 10 log10 (P1/P2) db
The two power values must be in the same units (kilowatts, watts, milliwatts,
microwatts - or horse power). If the ratio of the two power values is greater than
unity there is positive gain and if the ratio is less than unity there is negative
gain or loss. A ratio of unity of course gives zero gain.
Since it is usually more convenient to measure voltage or current values than
it is to measure the power directly, when the power is proportionate to the square
of the current or voltage, as in a circuit of pure resistance,
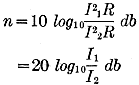
Likewise,
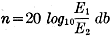
Strictly these relations hold only so long as the circuit conditions are the
same for the two measurements of either current or voltage. As has been pointed
out in a previous publication2 a correction must be applied where the
conditions are different for the two measurements. This will work no hardship in
most cases, however, especially where we are concerned with changes in power level
at only one point in a circuit. This will be generally true in amateur problems.
Because of the logarithmic character of the decibel, successive gains and losses
expressed in db are added algebraically. For instance, suppose we have a system
containing successively an amplifier giving a positive gain of 20 db, a line having
a negative gain (loss) of 5 db, an impedance-matching network giving a negative
gain (loss) of 30 db, and ending up with an amplifier contributing a positive gain
of 10 db. The overall gain of the system, from the input of the first amplifier
to the output of the terminating amplifier, would be. +20db-5db-30db+10db = -5db.
This feature in itself contributes considerably to the simplification of power level
calculations where there are a number of pieces of equipment between the input and
output terminals of a system. Once the gain for each piece of equipment is known,
providing the couplings have proper characteristics, it is necessary only to perform
a simple addition to determine the gain for the whole system.
Eliminating the Math
Now that we have dutifully traced the mathematical evolution of the decibel -
we trust it has been followed just as dutifully - the time has come to disclose
the inevitable short cut which eliminates the mathematical computations involving
log tables, slide rules, and such. The method is graphical and employs another mathematical
trick. Using "semi-logarithmic" graph sheets on which the ordinates form a geometric
progression while the abscissae form an arithmetical progression, power and current
or voltage ratios are plotted against db values, the resultant curve being a straight
line. Figs. 1 and 2 illustrate such graphical tables covering power ratios from
one one-millionth to a million with corresponding db values of from -60 to +60.
They also cover voltage or current ratios of from one one-millionth to one million
with corresponding db values of from -120 to + 120. These ranges are adequate for
all practical purposes since it is quite unusual to encounter gains or losses greater
than these values. Since the graphical tables reproduced here are somewhat small
for practical work, it is recommended that they be used as models for larger ones
plotted on graph sheets of the semi-logarithmic type, such as Keuffel & Esser
No. 358-72L. These sheets can be obtained in stores that handle draftsman's supplies.
The preparation is quite simple, consisting only of the notation of the coordinates
and the drawing of the diagonal straight lines. It would be less confusing, perhaps,
if separate sheets were used for ratios below 1000 ("A" curve) and over 1000 ("B"
curve) of Fig. 1, and for the "A" and "B" curves of Fig. 2. Then there
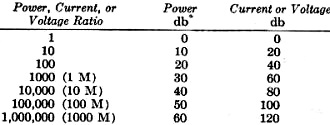
would be but one curve on each sheet. The following table can be used in plotting
the points for the curves:
The ratios are marked on the logarithmic vertical scales and the db values are
marked on the horizontal linear scales. Coordinates designated "A" are used for
the "A" curves and coordinates designated "B" are used for the "B" curves.
Once the curves have been plotted they can be used directly for translating power,
current, and voltage ratios to db values; or they can be used for translating known
db values to power, current, and voltage ratios. They work either way and completely
eliminate the bother of juggling logs and antilogs. Let's try a few examples.
R may be a 500,000-ohm potentiometer, preferably of the "tapered" type giving
a logarithmic resistance vs. knob rotation curve, as explained in the text. R1
is the usual cathode bias resistor used with heater type tubes and condensers C1
serve as by-passes.
Some Practical Applications
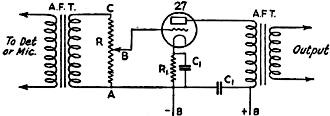
Fig. 3 - A Simple Type of Volume Control Which Can Be Calibrated
to Indicate Power Level
One of the things in which every amateur is vitally interested is the probable
improvement in performance accompanying a change in his transmitting equipment.
Who has not made adjustments that have resulted in increased output, as measured
by the antenna ammeter, and then found that there has not been a proportionate improvement
in signal strength as measured in audibility by a distant observer? Suppose we take
a typical example and see how it works out.
Without changing the frequency or antenna tuning adjustments, the plate voltage
on the transmitting tubes is raised so that the antenna current increases from 1
ampere to 1.5 amperes (representing a power increase of 2.25 times). What should
be expected in the way of improvement in signal strength, other things remaining
unchanged? The current ratio is 1.5, which, from curve"A" of Fig. 1, is seen
to represent a gain of 3.5 db. Remembering that the least increase in level that
is detectable by the ear is 1 db and that it takes as much as 2 or 3 db increase
to make a showing in the presence of QRM, etc., it is obvious that the increase
of 50% in antenna current will not do much more than bring the signal up about one
notch in the "R" scale of audibility. If the signal were R4 with 1 ampere antenna
current, it wouldn't be much over R5 with 1.5 ampere in the same antenna at the
same frequency. Of course this is neglecting the non-linear response characteristic
of the receiver (regenerative detector sensitivity is much greater for weak signals),
but even then the increase in signal strength is more nearly represented by the
gain in db than by the showing on the antenna ammeter.
Here is a more general problem. Suppose Bill Jones is contemplating building
a new transmitter to replace his present Type '10 outfit which has an output of
10 watts. What improvement in signal strength could he expect from a set using a
Type '52 and putting 100 watts into the same antenna system and on the same frequency?
The power ratio is 10 and the gain is 10 db, as an inspection of curve "A" of Fig. 1
will reveal. This gain will represent something like 3 or 4 steps in audibility
on the R scale so that if his signals were around R4 at Washout, N. D., with the
old outfit, he might expect R7 and R8 with the larger outfit under the same conditions.
Or suppose we wish to know the improvement that can be expected with an increase
in the modulation capability of a phone. transmitter.
The power of the modulator is increased so that the modulation capability is
made 90% instead of 30%, the carrier power remaining the same. What is the gain
in db? Since the antenna current amplitude is proportional to the percentage of
modulation, the improvement in modulation capability will represent a current ratio
of 3. From curve "A" of Fig. 1 it is seen that this is a gain of nearly 9 db
- no mean improvement in the sock of that particular phone set.
Passing on from the transmitter itself to the antenna system, suppose that W2SOX
decides to add a little directivity to his 28-mc. antenna and that the particular
combination he decides upon gives a rated gain of 6 db in the direction towards
which he wishes to push his signals. To what is this equivalent in terms of power
increase in a non-directive transmitting antenna? Consulting Fig. 1, curve"A,"
we find that the power ratio for a 6 db gain is 4. The directive antenna, therefore,
gives him the same increase in signal strength as he would obtain by increasing
the power - in the non-directive antenna to 4 times its normal value. Since the
array necessary to give this gain might consist of nothing more elaborate than two
"couplets," each consisting of a half-wave antenna-backed up by a reflector spaced
a quarter-wave behind it, with the two antennas excited in phase, it is obvious
that directive transmission is decidedly advantageous.
The Standard Reference Level
The decibel is primarily a unit that is used to specify gains and losses with
reference to the power value at some point in a system, irrespective of what the
actual value of the reference power may be. Since the unit is based on a power ratio,
however, it is natural to assume a standard reference power value and use the db
to express amounts of power as being so many db above or below this value. Several
reference levels have been more or less generally used, but the standard in broadcast
and allied fields at the present time is 0.006 watts or 6 milliwatts. When a broadcast
engineer says that a microphone is"30 db down" or that his level is "plus 8 db,"
he has this reference power in mind. Practically all the broadcast and telephone
equipment used in this country at the present time is rated and calibrated on the
basis of this reference level. When a pick-up amplifier is rated as having a "maximum
undistorted output level of 6 db," it means that the power output is 6 db (power
ratio of 4) above 6 milliwatts or that it is 24 mw. A fairly accurate picture of
the meaning of loudness in terms of the standard reference level of 6 mw. can be
obtained from the following approximations: Good R9 signal strength on a telephone
headset is about +2 db; loud, loud-speaker volume is about +20 db. A reference level
of 10 mw. is sometimes used, but unless otherwise specified the reference power
of 6 mw. can be assumed.
Measuring Power Level
There are several types of audio-frequency power level measuring devices in general
use. One type which is self-contained and requires no battery supply for its operation
is that in which a rectifier type voltmeter is used as the indicating instrument
in conjunction with a variable attenuator made up of suitable resistors and calibrated
in db. This type is usually designed for operation across a 500-ohm line. A voltmeter
reading of 1.7a volts corresponds to zero db level for a reference power of 6 milliwatts
when the instrument is connected across a 500-ohm line. The voltmeter scale is calibrated
from -10 db to +6 db and the attenuator which is calibrated from 0 to 30 db further
extends the use of the instrument - something like connecting a resistance in series
with a low-range voltmeter to increase its range. The attenuator for this type of
indicator necessarily must be so designed as to present a constant input impedance
in order to prevent its affecting the frequency characteristic of the line to which
it is connected. The variable attenuator is usually of the"L" type in which a series
and a shunt resistance element are varied simultaneously. The design of attenuation
networks is a whole story in itself and will constitute a separate article in a
future issue of QST.
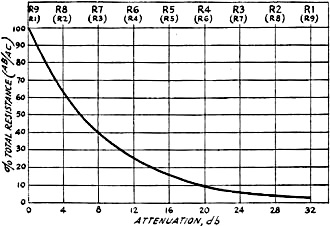
Fig. 4 - Illustrating the Relation Between volume-control
resistance ratio, db level, and audibility. The audibility figures in parentheses
suggest a calibration for audibility measurements on received signals. Details are
explained in the text.
A second type of power level indicator is that in which a vacuum tube is utilized
as a v.t. voltmeter. This type is more adaptable to amateur uses and has been treated
in a previous QST article.3 A modification of this arrangement is generally
used as the volume or "gain" control in amateur receivers and in the speech amplifiers
of phone transmitters, the attenuator being connected as a voltage divider in the
grid circuit of an audio amplifier as shown in Fig. 3. Such a simple attenuation
arrangement can be used only where there is practically no current flowing through
the resistor and where the impedance into which the attenuator system couples is
much higher than the resistance of the attenuator. These conditions are satisfied
in the grid circuit of an audio amplifier such as that illustrated. The position
of the sliding contact or tap-switch on the resistor R determines the value of the
signal voltage applied to the grid circuit of the amplifier tube, the ratio of the
voltage on the grid to the total voltage across the secondary of the transformer
being proportional to the ratio of resistance AB to the total resistance AC. But
the volume level will not be proportional to the ratio of the resistance values.
If the potentiometer is of the type having a straight-line resistance vs. knob-rotation
curve, the volume level will not be decreased noticeably until the gain has been
backed off about 1/3 of the total sweep of the knob. And there will not be a noticeably
rapid decrease in volume level with decrease of the resistance AB until the contact
has gone past the half-way mark. This is shown graphically in Fig. 4, where
attenuation in db has been plotted against per cent total resistance for a voltage
divider such as that shown in Fig. 3. A rough comparison of the resistance
ratios and signal strength in terms of the "R" system of audibility is also indicated
in Fig. 4, steps of 4 db each having been allowed for each step in the "R"
scale. The total attenuation between R9 and R1 is shown as 32 db, which may be taken
as a practicable approximation. Since the relation between resistance ratio and
volume level is a logarithmic one, it is obvious that the calibration of the potentiometer
scale should be logarithmic or that a logarithmic "tapered" resistor should be used.
The latter is the more practicable arrangement, since the scale calibration can
then be linear with respect to rotation of the control.
A receiver volume control having a logarithmic resistance characteristic could
be used to good advantage as an audibility meter by making its calibration the reverse
of the"R" scale shown in .the chart of Fig. 4 (as indicated by the parenthetical
figures). The angular scale could have ten divisions with "10" at the zero resistance
position and "1" at the maximum resistance position. A signal which was R9 would
just go out of audibility at the next position above zero resistance while a signal
that was R1 would be just audible with the resistor in the full "on" position. If
desired, the resistor could be calibrated in db instead of in "R" units of audibility.
The latter calibration would be especially applicable to the gain control of the
speech amplifier of a phone transmitter.
These are but a few of the many ways in which the db can be put to work in amateur
radio. Even to mention all the possible uses would run this story beyond page 98
- and it is long enough now. But we hope that the suggestions that have been made
and the information that we have tried to give will serve to further the adoption
of the db by amateurs. It is inevitable that we shall hear more of the thing, as
future QST articles will show. We cannot escape it. Perhaps it even may be heard
of over the air; "your sigs up 4 db now, OM - FB."
* Aviation Radio Station, Inc., 29 West 57th St., New York City.
1 Particularly "Some More About the Family," Chamberlain, QST, July, 1928; and
subsequent articles on volume level indicators, directive antennas, etc.
2 "Notes on Power Measurements in Communication Circuits," Crawford, General
Radio Experimenter, October, 1929
3 "Volume Level Indicators," Omer, QST, November, 1930; and correction in following
issue. Figs. 2 and 5 of this article should be interchanged.
Posted March 10, 2022
(updated from original post on 6/29/2016)
|