Basic Digital Logic Course - Part 1
|
|
This first of a three-part digital electronics series run by Popular Electronics magazine begins with introducing binary (base 2), octal (base 8), and decimal (base 10) number systems, along with conversions between the types. Sure, this is probably old-hat to most RF Cafe visitors, but there is always a new cadre of electronics enthusiasts entering the field who appreciate the instruction. No matter how advanced digital electronics gets, a fundamental understanding and fluency in binary arithmetic is essential to success whether as a hobbyists or as a professional. If you cannot move effortlessly between the various number formats (which also include hexadecimal and Gray code), then continuing to Boolean algebra and combinational logic and sequential logic circuits will be as futile as hoping to study circuit theory with knowing Ohm's law. See Part 1, Part 2, and Part 3. Basic Digital Logic Course - Part 1: Number Systems
The emergence of experimental digital IC projects has been so rapid that many people tend to get lost amid strange-sounding names like "quad 2-input positive NAND gate" and "BCD to 7 segment decoder/driver." Such terms describe the building blocks of digital electronics. To provide an introduction to logic for beginners and refresher information for more advanced experimenters, here is the beginning of a Digital Logic Course series. This first installment describes number systems and provides important background information for the next two installments. Number Systems. Early man was forced to count with small pebbles or knots on a string when he wanted to inventory his possessions. As time went on, and perhaps because he found it convenient to count with his fingers, man eventually devised a number system with ten digits. This provided a far more convenient and versatile counting system since, for example, the number 16 could be represented with merely two digits rather than 16 pebbles or knots. The comparatively recent development of electronic digital computers has revived interest in number systems based on something besides the decimal A system based on two digits is of particular importance in electronic digital computers. The reason for this is that an electronic circuit can be made to occupy only one of two states: on or off (saturated or cut off). Of equal significance is that any form of logic statement can be reduced to contain only true and false assertions. Since electronic circuits required to impalement true and false logic statements are very simple, a computer can be designed based on a two-digit number system, in which one digit corresponds to "true" and the other to "false ". The two-digit, or base-two, number system is called the binary system and its digits, called bits (for binary digits), are 1 and 0. The Binary System The easiest way to understand the binary system is to learn to count in binary fashion. One basic rule governs counting in any number system: record successive digits for each count until the count exceeds the total number of available digits; then start a second column to the left of the first and resume counting. Since the binary system leas only two digits, counting is very easy. You can prove this to yourself by counting to the equivalent of the decimal number 10 in binary. The binary of decimal 0 is 0. The binary of 1 is 1. Here the similarity ends. To express 2 in binary, you must start a new column since both binary, bits have been used in the first column. Hence, the binary of 2 is 10 (read one-zero - not ten). Three is expressed as 11 (one-one) in binary, which uses up both binary bits for the first two columns. So, a new column must be started for binary 4, which becomes 100, while 5, 6, and 7 become 101, 110, and 111. With 8, represented by the binary 1000, we must once again start a new column. Binary Arithmetic By learning how to count in binary, we have also derived three basic rules for addition: (1) 0 + 0 = 0; (2) 0 +1 = 1; and (3) 1 +1 =10(1 + 1 = 0, carry 1). These rules can be used to add any two binary numbers. For example, let us add 12 and 9 in binary:
Start with the right-hand column and add the least significant digit. Then continue adding each successive column, working from right to left, finishing up with the most significant bit:
Note in the above example that the addition of the two most significant bits yielded a 0 with a 1 carry. A carry can also occur within the addition as in: 1011 + 1101 = 11000. Converting Binary to Decimal Binary numbers are fundamentally easy to work with. But how do you convert a string of 1's and 0's to easily recognized decimal numbers? The process is simple, using a technique known as "expansion." Each digit column of a decimal number corresponds to a power of the base-10 to which it must be raised. Let us use the number 846 as an example:
A binary number can be expanded in the same way and converted into a decimal number. For example, let us expand (10111)2. The subscript denotes the base of the number system -in this case, 2 or "binary" - and helps in preventing confusion. The expansion is as follows:
Since the position of each digit in a binary number determines the power of 2 invoked, it is easy to convert binary to decimal simply by assigning the decimal equivalent to each column. A 0 in a column means that the column's power-of-2 decimal equivalent is not invoked. Therefore, the decimal equivalents of all columns containing a 1 are added to find the total decimal equivalent. Let us convert 10011 to decimal:
Manual binary arithmetic involving numbers containing more than three or four bits is both tedious and cumbersome when you are accustomed to counting in a decimal system. But an electronic computer can perform thousands of lengthy binary additions in fractions of a second. This ability is vital to the success of digital computers and calculators, since all arithmetic operations can be performed by addition or its variations. Subtraction is the inverse of addition, while multiplication is simply repeated additions and division is the inverse of multiplication. These facts about addition are important because they mean that even the most complicated arithmetic operations can be solved by addition. In practice, manual arithmetic rarely invokes this process. After all, you would find it inconvenient to multiply 641 by 197 if you had to write 197 times the number 641 and add the columns. But an electronic computer does the equivalent of this in only a few milliseconds. The Octal System. Sometimes binary numbers are condensed into other number systems to further simplify computer processing. Since the binary system has only two digits, it does not take long to accumulate a string of seemingly endless 1's and 0's. A decimal number with only two digits, for example, requires five binary bits. A six-digit decimal number requires 19 bits.
You can use a table of octal numbers and their binary equivalents to convert a long binary number such as 11101100001101 into octal. First, divide the number into groups of three bits each, beginning with the least significant bit: 11 101 100 001 101. Then assign the octal equivalent to each three-bit group, using the octal-to-binary equivalents given in the table:
Hence, (11101100001101)2 equals (35,415)8. It is obvious that the latter number is easier to process than the former. Sometimes the base-16 (hexadecimal) number system is used to further simplify long binary numbers. The hexadecimal technique requires that the binary number be subdivided into groups of four bits each, again starting with the least significant digit. The result is a hexadecimal number that is only a fourth the length of the original binary number. Next month, we will discuss logic concepts and circuits and demonstrate how logic circuits can be combined to make a binary adder.
Posted September 16, 2019 |
|
By Forrest M. Mims 
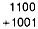
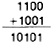
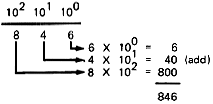
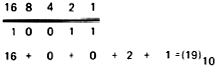
Complicated binary numbers can be simplified
by dividing them into groups of three or four bits and encoding the results in other
number systems. Since the binary numbers for the decimal digits 0 through 7 form
groups of no more than three binary digits each, a long binary number can be reduced
to a third of its length by converting it to a base -8, or octal, number system.
