Old and New Mathematical Puzzles
|
||||
I finally got around to scanning selected content from the 1986 issue of The Old Farmer's Almanac. The "Old and New Mathematical Puzzles" feature was always my favorite, so that's what is posted first. Difficulty levels are assigned as 1 for the easiest to 5 for the hardest. Solutions are provided for levels 1 through 4, but level 5 (problems 12 through 15) problems were to be mailed in (no e-mail in the day) to vie for a cash prize for providing the "best set of solutions," though I don't know how one solution to these problems can be deemed "better" than another. Problem #5 is interesting in that you must assign a value for the various numerical prefixes and quantities. Sure, we all know what "atto" and "score" are, but what about "crore" and "myriad?" Old and New Mathematical Puzzles Blanton C. Wiggin, Puzzle Editor From an above average group of readers' puzzles, we have selected 15 classical, original, or timely puzzles for 1986. They are graded for difficulty, so that there should be something of interest for everyone. We hope you find them challenging. No calculus, computers, or tricks. We try to include specialized knowledge, if needed, in the puzzle statement. Some puzzles may require a chart or table of data from your local library. We will award one prize of $50 for the best set of solutions to puzzles 12 through 15 received before February 1, 1986. The answers to these four are omitted here. We use a point system to judge the prize set. A basic, unadorned, correct answer is 20 points; for a thorough analysis, an elegant or novel answer, up to 5 points extra. Numerical errors lose only 2 or 3 points, if it is clear that the method is understood. Explanations and Prize - Set Answers will be sent after June 15 to anyone sending 50ยข and a self-addressed stamped envelope to "Puzzle Answers," The Old Farmer's Almanac, Dublin, New Hampshire 03444. We will also. pay $15 for any original puzzles we use in The Old Farmer's Almanac for 1987. Closing date for submissions is March 1, 1986. Entries become the property of Yankee Publishing Incorporated and cannot be acknowledged or returned. In addition to submitting a puzzle, please tell us the type of puzzle you like best, such as magic squares, geometry, time-rate-quantity, mazes, logic, number substitutions, etc. From a large group of good answers, we are happy to announce a second-time winner for 1985: Arthur Loepp of Kansas City, Missouri, with 97 points repeating his 1982 win. Runners-up were Leon Kreidler, Sheboygan, Wisconsin, last year's winner, 95 1/2; Tina Virzi, Plattsburgh, New York, 93 3/4; and Harvey Vigour, Waynesboro, Virginia, 93. Other high scorers were G.M. Hall, Alexandria, Virginia, and past winner Newton Amos, St. Louis, Missouri. Congratulations to all! Have a go at these 1986 puzzles and send your answers early for puzzles 12-15. Use a separate sheet for each puzzle or answer, and be sure each sheet has your name and address on it. Good luck!
Difficulty: 1 a. Relocate only 2 walls (toothpicks) and reduce 5 rooms to 4. b. A developer agreed to put in 5 roads with 4 houses on each road. The planning board allowed only 10 houses, yet he successfully completed his agreement. How? William W. Hurley: Princeton, W Va. and Paul Fidelet, Sudbury, Mass.
2. The Scrambled Salesman Difficulty: 1 An egg salesman sold his first customer half his crates of eggs and half a crate more. His second and third buyers took the same type of order. He filled all 3 orders, was sold out, and hadn't had to break a single egg or crate all day. How many crates had he sold? Jennifer Hughes, Pinconning, Mich. 3. Muffin Madness Difficulty: 2 Milly Miffen made a muffin more than Molly Murphy's mother Mabel made. Milly Miffen's mother Maida made a muffin more than Molly Murphy made. Milly Miffen, Molly Murphy's mother Mabel, Molly Murphy, and Milly's mother Maida Miffen made 50 muffins, but Milly Miffen and Molly's mother Mabel Murphy made four muffins more than Molly Murphy and Milly's mother Maida Miffen made. So murmur now how many muffins Milly made. Jerry Curtright, Carpemersville, Ill. 4. Third Millenium Lady Difficulty: 2 Julie will be X years old in the year X2. Her uncle was Y years old in the year Julie was born, having been born back in Y2! When were niece and uncle born? Rand Higbee, White River, S. Dak. 5. Curious Counting Difficulty: 2 So you think you learned to count when you were three or so? Maybe, but do you know these quantities - nouns or prefixes for cardinal numbers? All are part of the English lexicon, just as "score" is 20. ace __________________ atto- __________________ avogadro __________________ brace __________________ bundle __________________ centillion, Anglo-German __________________ centillion, Franco-American __________________ crore __________________ duodeci- __________________ e __________________ femto- __________________ fin __________________ giga- __________________ icosa- __________________ lakh __________________ long hundred __________________ love __________________ K- __________________ mega-micro- __________________ myriad __________________ nano __________________ nonad __________________ pi __________________ pico- __________________ ream, standard __________________ googol __________________ grand __________________ great gross __________________ heptad __________________ hexadec- __________________ shock __________________ tera- __________________ thou __________________ tre __________________ undeci- __________________ zip __________________ Some are used only in special fields, of course, but they all have a dimensionless, fixed numerical value. They do not represent physical properties, such as a gallon is so many quarts (volume), or miles-per-hour so many knots (speed), which have physical dimensions. Jackie Shoemaker, Waverly, Penna. 6. Dense Pack
Difficulty: 3 Tom is stacking perfectly round logs in a certain rectangular space, and he wants to pack them as tightly as he can with all the logs exactly the same diameter. Will the stack be more dense if he uses logs of smaller diameter or greater diameter? Bill MacCartney, Ashby, Mass. 7. Triplets Hop Difficulty: 3 Jigsaw and Sawjig are 6-digit numbers. If 6 times Jigsaw = 7 times Sawjig, what is the value of each letter? Peter Voorheis, Friendship, L. I. 8. Almanacryptogram Difficulty: 3 a. Work out these anagrams about 1986. Ignore the underlinings for now. YELLAH STRUNER HITS RAYE b. Using the new letters falling into the underlined positions, make a related word in the numbered spaces. ___ ___ ___ ___ 1 2 3 4 c. Put these letters into the numbered spots in this cryptogram. They may also go elsewhere. Solve. V UQZ1Y WDSGT2KK QD WSPINXZD WL3XW KQLX WYBYMY V WPHXZ WHXAIVA4X CVLXW. Erma Nightingale, Newton Highlands, Mass. 9. Squares, Cubes, and Factors Difficulty: 4 a. A certain characteristic enables a number to be both a perfect square and a perfect cube, How many such integers are there less than one million? b. What is the smallest integer which is the sum of two cubes, in two different ways? c. Is there an integer less than b. which, squared, is the sum of two squares, in four different ways? d. What is special about the number 2520? John H. Hitchcock, Princeton, Mass. and Richard Burgess, Lonoke, Ark. 10. Deductions Difficulty; 4 Each offour men was given a similar appearing closed box, and the contents list of one of the other boxes. Each box contained 3 colored balls in unique assortments: BBB; BBW; BWW; WWW Each man knew this, saw only the one list, but in turn opened and announced the first two balls he withdrew from his box. He then tried to deduce the third, still unseen color in the box. Said Art, "I drew 1B, 1W, and I know the third." Bob: "I pulled out 2B, and I know the third." Cal announced he had 2W, third unknown. Don was blind, but correctly announced his 3 and all other remaining colors. What were they? /p> John A. Robbins, Falmouth, Mass. 11. Missin' Digits Difficulty: 4 Fill in the blanks. The answers can be reasoned out. No left-hand zeros, please.
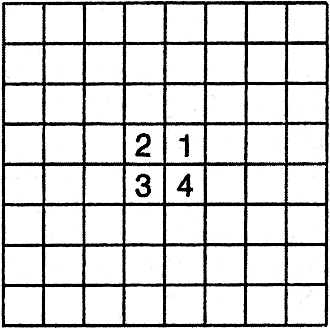
Dorothy J. Johnson, Brookfield, Wis. 12. Quadrant Square Difficulty; 5 Just as I, II, III, IV describe trig-geometric quadrants, they can be the starting numbers for an 8-order magic square. All horizontals, verticals, and major diagonals add to the same number. Each 4-square quadrant adds similarly to a number. Use the quantities 5 to 64 once and only once in the empty boxes.
Alvis King, Orleans, Ind. 13. Scrolling Digits Difficulty; 5 Scrolling signs are like the one on the old Flatiron Building in Times Square, New York, continuously stepping to the left in a long loop before repeating. Here are some numbers which scroll to the right one place and stop. IMAGE HERE Question: What series of digits, when multiplied by 6, scrolls? Have some fun with this simple new concept. Your answers and whatever else you discover about scrolling will be considered in your Prize Set answer. Gary Baird, Carthage, Mo. 14. Heptagon Hex Difficulty; 5 With center at O, describe circle of diameter AH. Using A and H as centers, and radius AH, construct arcs intersecting at I. Now draw any straight line through A except concurrent with AH or AI. Mark off 7 equal segments ending in A'. Draw A'H and construct parallels from AA', dividing AH into 7 equal segments at B, C, D, E, F, & G. Construct IC and extend to circle O at J. Using chord AJ as a length, construct equal chords JK, KL, LM, MN, etc. What have you drawn? Norton Black, Tucson, Ariz. 15. Cross Number A Difficulty: 5 a. Many people like crossword puzzles, so here are a pair of analogous stumpers using only numbers. Same rules. Any numbers too long for the space are rounded in normal fashion to the nearest value. Please ignore decimal points.
1. Mantissa of log 5. 370 squared 9. MDXXVII 10.April 24's day of 1986 11. This digital root = 0 12. Old long distance 13.This digital root = 1 15. 4th root of 614,656 16. East Boston (Mass.) zip 18. Hexadecimal base 19. Product of 2 primes each ending in 1 21. A lakh 23. Hastings' binary year 225. Consecutive digits 26. Odometer showing a seventh of the square root of 240,100 27. Unlucky number 28. Hollywood (Calif.) zip 30. Duo-decimal base 32. New emergency # 33. 164 in duo-decimal 34. End of T'ang Dynasty 35. Semi-circle degrees 36. Pearl Harbor minus 30 37. mm/100 inches plus inches/10 kilofeet plus a score 38. IV x MCLXXVII Down
b. Topsy-turvy Cross Number This puzzle works both right-side-up and upside-down. Thus you can use only 0, 1, 6, 8, or 9. No left-hand (leading) zeros, such as 06, permitted. No digit appears more than 3 times in either orientation. No single-digit numbers. Sorry, but we lost some of the clues and clue numbers! Not to worry; these are all you need:
b. Product of two numbers in the puzzle. c. 1 across, 4 across, 12 across, and 14 across have a common factor larger than this. d. There is only one perfect square. Samuel W Eliot, Oklahoma City, Okla. and Bob Lodge, Seattle, Wash. Answers to Old and New Mathematical Puzzles 1. a. b. 2. 7:4, 2, & 1. 3. 14 4. 1980, 1936 5. 1, 10-18,602 X 1021, 2, 103, 10600, 10303, 107, 12, 2.718,10-15, 5, 109, 10100, 103, 1728, 7, 16, 20, 105 120, 0, 103, 106, 10-6, 104 10-9, 9, 3.142, 10-12, 500, 60, 1012, 103, 3, 0. 6. Smaller. 7.6 x 538461 = 7 x 461538 8. A dirty snowball in southern skies like SYZYGY a super spectacle makes. 9. a. 9; the sixth powers of integers 1 through 9, only. b. 1729 = 13 + 123 = 93 + 103. c. Yes. 1625 = 572+16242 = 4002 + 15752 = 8252 + 14002 = 11132 + 11842. d. Lowest number divisible by 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10. 10. IMAGE HEREDetails of reasoning in "Explanations and Prize Set Answers." 11. a. Many answers. b. For one: 12,128,316 ÷ 124 = 97,809 12-15. Prize Set. See instructions on p. 190.
See answers below ---
Posted January 28, 2021 |
||||
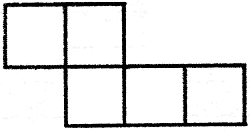1. Less Housing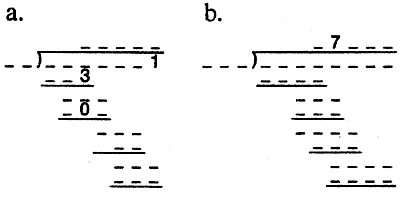 
Across 
a. The year of this OFA. 