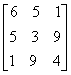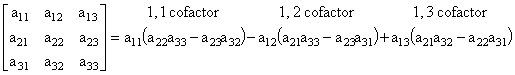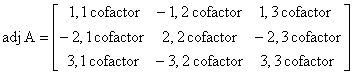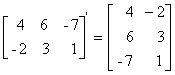Electronics World articles Popular Electronics articles QST articles Radio & TV News articles Radio-Craft articles Radio-Electronics articles Short Wave Craft articles Wireless World articles Google Search of RF Cafe website Sitemap Electronics Equations Mathematics Equations Equations physics Manufacturers & distributors Engineer Jobs LinkedIn Crosswords Engineering Humor Kirt's Cogitations Engineering Event Calendar RF Engineering Quizzes USAF radar shop Notable Quotes App Notes Calculators Education Engineering Magazines Engineering magazine articles Engineering software Engineering smorgasbord RF Cafe Archives RF Cascade Workbook 2018 RF Stencils for Visio RF & EE Shapes for Word Advertising RF Cafe Homepage Sudoku puzzles Thank you for visiting RF Cafe!
Innovative Power Products Couplers

Matrix Definitions

In mathematics, a matrix (plural matrices, or less commonly matrixes) is a rectangular array of numbers, as shown at the right. One use of matrices is to keep track of the coefficients in a system of linear equations. Matrices can also represent linear transformations, which are higher-dimensional analogs of linear functions of the form f(x) = cx, where c is a constant. They can be added and subtracted entrywise, and multiplied according to a rule corresponding to composition of linear transformations. These operations satisfy the usual identities, except that matrix multiplication is not commutative: the identity AB=BA can fail. For a square matrix, the determinant and inverse matrix (when it exists) govern the behavior of solutions to the corresponding system of linear equations, and eigenvalues and eigenvectors provide insight into the geometry of the associated linear transformation.

Matrices find many applications. Physics makes use of them in various domains, for example in geometrical optics and matrix mechanics. The latter also led to studying in more detail matrices with an infinite number of rows and columns. Matrices encoding distances of knot points in a graph, such as cities connected by roads, are used in graph theory, and computer graphics use matrices to encode projections of three-dimensional space onto a two-dimensional screen. Matrix calculus generalizes classical analytical notions such as derivatives of functions or exponentials to matrices. The latter is a recurring need in solving ordinary differential equations. Serialism and dodecaphonism are musical mouvements of the 20th century that utilize a square mathematical matrix (music) to determine the pattern of music intervals. - Wikipedia
 
UnityElementarySymmetric
Matrix Definitions Unity - RF Cafe
Diagonal Matrix with main
diagonal elements = 1		Matrix Definitions Elementary - RF Cafe
All elements = 0 except
for  a single 1
Matrix Definitions Symmetric - RF Cafe
Square Matrix with
aij = aji
SquareDiagonalNull
Same number of rows and columnsMatrix Definitions Diagonal - RF Cafe
Square Matrix with
aij = 0 for all i¹ j

Matrix Definitions Null - RF Cafe
All elements = 0
Singular
Value of determinant = 0


Determinant
Matrix Definitions Determinant - RF Cafe

Adjoint
Matrix Definitions Adjoint - RF Cafe

Square Matrix where aij is replaced with I, j cofactor multiplied by (-1)i·j.
Adjoint A = adj A

Rank
  • Maximum number of linearly independent columns of the matrix A.
  • Order of the longest nonsingular matrix contained in matrix A.

Rank of A = Rank of A'    
Rank of A = Rank of A'A  
Rank of A = Rank of A A'

 

Transpose
Matrix Definitions Transpose - RF Cafe

Matrix where rows and columns are interchanged.

Transpose A = A

(A')' = A
(kA)' = kA'
(A+B)' = A'+B'
(AB)' = B'A'



Windfreak Technologies PCB Directory (Design)
Exodus Advanced Communications - RF Cafe vidaRF RF & Microwave Components - RF Cafe
About RF Cafe
Kirt Blattenberger - RF Cafe Webmaster
Copyright: 1996 - 2024
Webmaster:
    Kirt Blattenberger,
    BSEE - KB3UON

RF Cafe began life in 1996 as "RF Tools" in an AOL screen name web space totaling 2 MB. Its primary purpose was to provide me with ready access to commonly needed formulas and reference material while performing my work as an RF system and circuit design engineer. The Internet was still largely an unknown entity at the time and not much was available in the form of WYSIWYG ...

All trademarks, copyrights, patents, and other rights of ownership to images and text used on the RF Cafe website are hereby acknowledged.

My Hobby Website:  AirplanesAndRockets.com

spacer