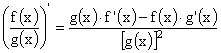|
||||||||
|
||||||||
Differentiation Rules |
||||||||
|
In calculus, a branch of
mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a
derivative can be thought of as how much a quantity is changing at a given point. For example, the derivative of
the position (or distance) of a vehicle with respect to time is the instantaneous velocity (respectively,
instantaneous speed) at which the vehicle is travelling. Conversely, the integral of the velocity over time is the
vehicle's position. The derivative of a function at a chosen input value describes the best linear approximation of the function near that input value. For a real-valued function of a single real variable, the derivative at a point equals the slope of the tangent line to the graph of the function at that point. In higher dimensions, the derivative of a function at a point is a linear transformation called the linearization. A closely related notion is the differential of a function. The process of finding a derivative is called differentiation. The fundamental theorem of calculus states that differentiation is the reverse process to integration. - Wikipedia
|
||||||||
|
 |
 |
 |
 |
| About RF Cafe | |
 Copyright: 1996 - 2018 Webmaster: Kirt Blattenberger, BSEE - KB3UON |
|
|
RF Cafe began life in 1996 as "RF Tools" in an AOL screen name web space totaling 2 MB. Its primary purpose was to provide me with ready access to commonly needed formulas and reference material while performing my work as an RF system and circuit design engineer. The Internet was still largely an unknown entity at the time and not much was available in the form of WYSIWYG ... All trademarks, copyrights, patents, and other rights of ownership to images and text used on the RF Cafe website are hereby acknowledged. My Hobby Website: AirplanesAndRockets.com
|
|
