A.C. Negative-Resistance Devices
|
|
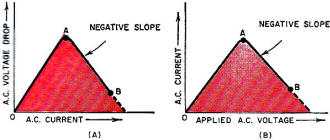
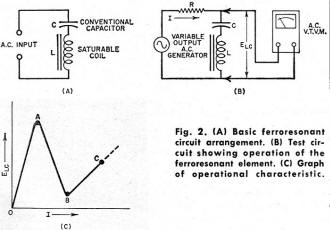
Most RF Cafe visitors are familiar with the negative resistance region exhibited in tunnel diodes. It is what makes them usable, among other special applications, as oscillators. Although a diode is often part of an AC circuit, it is fundamentally thought of as a DC device since it permits conduction in only one direction (the exception being a Zener diode). An AC device in general refers to something used in a line supply circuit at 50 Hz, 60 Hz, or even 400 Hz. Such is the case with this article, which describes negative resistance characteristics of voltage-variable capacitors (varactor) and ferroresonant devices like saturable coils. See author's "Negative Resistance: What It Is & How It's Used" article in the May 1961 Electronics World. A.C. Negative-Resistance Devices Description of ferroresonators, nonlinear-type capacitors, semiconductor capacitors, and other similar components. By Rufus P. Turner The author's earlier article on negative resistance was devoted to direct-current devices.1 However, that article stated in conclusion that certain a.c. devices also exhibit the property of negative resistance, or negative impedance. This article describes devices of this type. For simplicity's sake, throughout this article the term "negative resistance" will be used in a generic sense. But the reader will recognize that the negative quantity may be impedance or reactance, rather than resistance. Such a.c. negative-resistance devices are not nearly as numerous as the d.c. devices, but we may reasonably expect additions to the family as research and development continue. The external manifestations of a negative characteristic are substantially the same in a.c. and d.c. devices, that is, the conduction curve has a negative slope over some part of it. In one instance, current will be the independent variable; in another, voltage will be. Thus in Fig. 1A, current is the independent variable. As the a.c. current is continuously increased, the a.c. voltage drop across the device first increases from 0 to A and then decreases (showing a negative resistance) from A to B. In Fig. 1B, voltage is the independent variable. As the applied a.c. voltage is continuously increased, the a.c. current flowing through the device first increases from 0 to A, and then decreases (showing negative resistance) from A to B. The following sections describe the action of devices which exhibit one or the other of these conduction characteristics. Ferroresonator Fig. 2. (A) Basic ferroresonant circuit arrangement. (B) Test circuit showing operation of the ferroresonant element. (C) Graph of operational characteristic. The ferroresonator (also called "ferroresonant circuit," saturable-reactor switch," and "ferristor") is a special type of series-resonant LC circuit. It really is quite simple, consisting only of a coil and capacitor connected in series (see Fig. 2A). The capacitor is a conventional one but the coil is not. The special feature of the coil is its core which saturates readily. Because of core saturation, the inductance and reactance of the coil decreases as the current is increased. An ordinary iron-core filter choke will exhibit saturation and a resulting decrease in inductance if current is raised high enough, but this usually requires a rather large current at power-line frequencies. A ferroresonator coil intended for operation between 100 kc. and several megacycles, however, is wound on a tiny, thin core of high-permeability metal and will saturate on only a few milliamperes. The LC combination resonates at a frequency, fr, determined by the
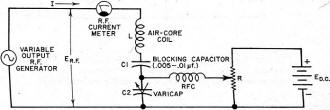
inductance and capacitance values. (Resonant frequency Fig. 2B shows a typical ferroresonant circuit. Here resistance R is non-inductive. The generator provides an adjustable a.c. output voltage. By adjusting the voltage, the operator varies current I flowing through R, L, C in series. The voltage (ELC) across the LC combination is measured with a high-impedance a.c. vacuum-tube voltmeter. Fig. 2C shows circuit response. As the current is steadily increased, voltage ELC rises to a peak (point A), then decreases to a valley (point B), and finally rises again to C and beyond. Thus, AB is a negative-resistance region bounded by two positive-resistance regions (0A and BC). This is a typical negative-resistance curve. The circuit behavior may be explained in the following manner. (1) The L and C values are selected to give a resonant frequency somewhat lower than the generator frequency. Increasing the current decreases inductance L and tunes the circuit up to the generator frequency and finally to some still higher frequency. (2) As I is increased from zero, ELC rises and would continue to do so if the core of the coil did not begin to saturate. Saturation (starting at point A in Fig. 2C) lowers the inductance and tunes the circuit toward resonance at the generator frequency. (3) At generator resonance, the net reactance of the LC combination is theoretically zero, therefore ELC is theoretically zero. As resonance is approached, ELC accordingly decreases. At resonance (point B), ELC does not drop fully to zero because resistance losses remain to act in the circuit after resonant cancellation of the reactance. (4) As I is increased further, core saturation increases, inductance lowers still more, and the circuit is tuned to a frequency higher than the resonant frequency. Thus, the voltage once more rises - in this case from B to C. Tiny r.f. ferroresonators have been used as active elements in flip-flops, electronic counters, gates, and other computer-type devices.2,3,4 They also have been employed as magnetic amplifiers at audio frequencies. In these particular units, C usually is a fairly small mica capacitor, while L is a coil that has been wound on a core of Permalloy foil. Nonlinear Capacitor Element Fig. 3. (A) Basic circuit arrangement using a nonlinear capacitor. (B) Test circuit showing operation of the nonlinear element. (C) Response of the test circuit. Fig. 4. Alternative circuit with a semiconductor capacitor. Fig. 3A shows a series-resonant negative-resistance circuit which resembles the ferroresonant circuit described in the preceding section but behaves somewhat differently. This arrangement uses a conventional air-core coil and a nonlinear (voltage-variable) capacitor. Suitable capacitors of this type contain a high-K ceramic dielectric, such as specially processed single-crystal barium titanate. As the voltage applied to the capacitor is increased, the capacitance decreases. As in the standard ferroresonant circuit, the L and C values in Fig. 3B are selected so that the zero-voltage resonant frequency of the circuit is lower than the generator frequency. As the voltage is increased, the current rises from zero to a peak point (A in Fig. 3C). As the voltage is increased further, the current decreases. Thus, the current-voltage curve has a negative slope from A to B. Behavior of the circuit may be explained in this manner. (1) The increasing voltage lowers the capacitance and tunes the LC circuit up toward the resonant frequency (generator). The current increases because increasing capacitive reactance causes the net reactance of the circuit to decrease. (2) At resonance with the generator, the net reactance is theoretically zero, and maximum current flows. This corresponds to point A in Fig. 3C. (3) As the voltage is increased beyond this point, the circuit is tuned to frequencies higher than resonance. The capacitance continues to fall but the net reactance of the circuit increases, so the current decreases. This is represented by the negative slope, AB. Semiconductor Capacitor Circuit A ceramic nonlinear capacitor, such as C in Fig. 3, usually requires relatively high-voltage operation for appreciable capacitance change. Furthermore, such capacitors are quite temperature-sensitive because of the Curie point of the dielectric material. To obtain low-voltage operation (from a few tenths of a volt to 1 to 6 volts r.m.s.) and at the same time to secure comparative freedom from temperature effects, semiconductor voltage-variable capacitors may be substituted in the circuit, as shown in Fig. 4. Response is the same as that shown in Fig. 3C. In Fig. 4, the semiconductor voltage-variable capacitor (also known as Varicap, varactor, Semicap, etc.) is d.c.-biased in a reverse direction to set its initial capacitance to a desired value and to prevent positive peaks of the maximum r.f. voltage from driving the semiconductor junction into the low-resistance forward direction. C1 is a blocking capacitor to keep d.c. out of the current meter and generator. As in the preceding example, values of L and C2 are chosen for zerosignal resonance below the generator frequency. Because the capacitance of C1 is very high with respect to that of C2, it has negligible effect on circuit tuning. Nonlinear Parallel-Resonant Circuit It is well known that the current in the line supplying a parallel-resonant circuit dips to a low value when the circuit is tuned to resonance at the generator frequency. If a voltage-tuned element is included in the parallel-resonant circuit, the circuit will then resonate at only one value of input voltage. The line current will then decrease at this voltage level, showing a negative slope. Fig. 5A shows a circuit for displaying this negative-resistance effect. The parallel-resonant circuit is composed of air-core coil (L) and a 56 pf. (μμf.) Varicap semiconductor voltage-variable capacitor (C2). C1 is a blocking capacitor (0.005 to 0.01 μf.) whose capacitance is so high with respect to C2 that only the latter determines the circuit tuning. The values of L and C2 are chosen such that the zero-signal-voltage resonant frequency of the circuit is somewhat lower than the generator frequency. As the generator voltage (ER.F.) is increased, the current (IR.F.) increases from zero to point A in Fig. 5B. The increasing voltage reduces the capacitance of C2. At the particular level of signal voltage, the corresponding C2 value tunes the circuit to resonance at the generator frequency, and the line current dips to point B. As the voltage is increased further, the capacitance decreases still more, tuning the circuit above resonance, and the current again rises to point C and beyond. Along the negative slope, AB, the current is decreasing as voltage is increasing. For best results, the generator frequency should not be lower than 20 mc. The higher the frequency, the more pronounced is the negative-resistance effect. Diodes at Higher Frequencies At high radio frequencies, the combined action of nonlinear capacitance and a.c. rectification provided by the semiconductor voltage-variable capacitor gives rise to an a.c. negative-resistance effect (as well as to hysteresis, in some cases). Heizman has described a microwave setup in which the capacitor diode is operated in a tunable waveguide.5 The negative resistance and hysteresis obtained with this arrangement have been utilized for switching at microwave frequencies. The response curve is similar to those of Figs. 1B and 3C. The conventional point-contact germanium diode has been known to exhibit negative resistance at very high frequencies. North observed that individually welded whisker diodes showed this effect when used as v.h.f. superhet converters.6 Such a.c. negative resistance has been observed in some conventional diode tubes operated at u.h.f.7,8 This is a secondary effect resulting from electron transit time in the tubes. The mechanism involves the dynamic plate resistance of the diode, which decreases at ultra-high frequencies. When the transit time equals the period (1/f) of the applied voltage, Rp = 0. At higher values of transit time, Rp is first above then below zero, its oscillating curve showing a negative slope in some portions. Feedback Amplifiers An amplifier provided with the proper amount of positive feedback may present negative resistance to circuitry connected to its input terminals. This applies to amplifiers of all types, such as vacuum-tube, transistor, magnetic, dielectric, and varactor. It is this very property that is utilized so widely in oscillating and regenerative circuits; the negative resistance provided by the feedback amplifier cancels the losses of the tank circuit into which it operates. A familiar example, in which loss cancellation results in a large increase in figure of merit, is the "Q"-multiplier. The grounded-grid amplifier operates very effectively as an a.c. negative-resistance device and has been exploited in telephony as a two-way repeater. A general limitation of all a.c. negative-resistance devices is their requirement of an a.c. supply, which is sometimes inconvenient and which always limits the maximum speed at which the device operates. When a.c. supply and circuitry are already provided, however, or the application is of an a.c. nature to start with, and the supply frequency is high enough to permit maximum desired operating speed, a.c. negative-resistance devices offer distinct advantages. References 1. Turner, Rufus P.: "Negative Resistance: What It Is & How It's Used," Electronics World, May 1961. 2. Isborn, Carl: "Ferroresonant Flip-Flops" Electronics, April 1952 3. Rutishauser, R. W.: "Ferroresonant Flip-Flop Design," Electronics, May 1954. 4. Triest, W. E.: U.S. Patent No. 2,709,757 (May 31, 1955). 5. Heizman, C. L.: "Microwave Bistable Circuits Using Varactor Diodes," Proceedings of the IRE, April, 1961. 6. Torrey. H. C. & Whitmer, C. A.: "Crystal Rectifiers," McGraw-Hill Book Co., New York, 1948, pgs. 362, 391. 7. Llewellyn, F. B. & Bowen, A. E.: "The Production of Ultra-high-frequency Oscillations by Means of Diodes," Bell System Technical Journal, April 1939. 8. McPetrie, J. S.: "A Diode for Ultra-H-F Oscillations," Experimental Wireless and Wireless Engineer, March 1934.
Posted February 7, 2017 |
|

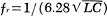 . Capacitance C is constant,
but inductance L varies with the current, I, flowing through the circuit, so the
resonant frequency changes with current. (As I increases, L decreases, and fr
increases.) This is the basis of Ferroresonator operation.
. Capacitance C is constant,
but inductance L varies with the current, I, flowing through the circuit, so the
resonant frequency changes with current. (As I increases, L decreases, and fr
increases.) This is the basis of Ferroresonator operation.