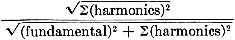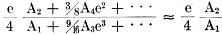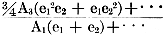Two Ways to Measure Distortion, October 4, 1965 Electronics Magazine

Here is a good, brief introduction to harmonic and intermodulation distortion measurement methods that were commonly used in the 1960s. Total harmonic distortion (THD) was used often, especially for audio equipment, which of course most frequency conversion circuits ultimately were in the era since digital data transmission over the air was not too common. Author Charles Moore worked for Hewlett-Packard (HP) and references HP Application Note 15, "Distortion and Intermodulation" which, thankfully, is made available by The HP Memory Project website. In fact, a complete list of all the vintage app notes are available on this page by downloading the PDF files. I highly recommend that you download and save all you think you might ever want because as with most things on the Web, they could disappear at any time. Some have been captured on the Archive.org website (I just now had it save AN-15 for time immemorial).

Its cause, system nonlinearity, may be calculated from the output harmonics of a single signal, or from the intermodulation of two.

The goal of audio and communications equipment is to reproduce input signals faithfully at the output. But system nonlinearity changes the waveshape of the signals; the resulting additional frequencies at the output are a measure of the distortion. Poor reproduction brought about by distortion will appear to the user of audio equipment as a change in the quality of musical instruments, or as noise; to the user of communications gear, it may also appear as channel crosstalk

It is necessary to identify nonlinear distortion before it can be eliminated. Two methods are in common use - total harmonic distortion analysis and intermodulation distortion analysis. The choice depends primarily on the characteristics of the system being tested and the information desired.

Output signal of nonlinear system, with the fundamental filtered out, is the lower trace on the oscilloscope screen. The residual output shows that seemingly pure sine wave does in fact contain harmonics.

Each input to a perfectly linear system produces a proportional output. For example, if an input f₁(t) produces an output g₁(t), and a second input f₂(t) produces an output g₂(t), the sum, f₁(t) + f₂(t), must produce g₁(t) + g₂(t) at the output. The output of the system can then be defined as

where F (jω) is the frequency spectrum of f(t), G (jω) the frequency spectrum of g(t), and H(jω) the transfer function of the system, which has finite gain at all frequencies. For every perfectly linear system, therefore, all frequencies in the input will appear at the output, changed only by a scale factor; no frequency that is not in the input can appear at the output.

For a perfectly linear amplifier, the expression is e_o = Ae_in, where e_in is the voltage at the input, e_o the voltage at the output, and A the transfer function - in this case the gain of the amplifier. A nonlinear amplifier, however, produces harmonics at the output, which can be characterized by the power series expansion of its transfer function:

The purpose of any distortion measurement is to determine the value of the coefficients of the terms in the series. As an example, if the input signal is

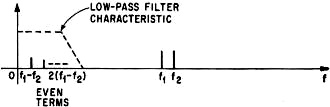
If proper care has been taken during the design of a system, nonlinearity will not be too severe. It is practical to assume that the distortion is less than 10%, so the terms of the expansion higher than the third power have been neglected.

Analysis of the series expansion shows that the relative amplitude of the second and third harmonic terms generated will vary directly with the input signal level. For second harmonics, the amplitude is proportional to e₁² or e₂². These terms will, therefore, vary 2 decibels per decibel of signal level change. Correspondingly, the third harmonic terms will vary 3 db per decibel of signal. level change.

For the intermodulation terms, a frequency of the form aω₁ + bω2 varies as e₁^|a| e₂^|b|. For example, the frequency 2ω₁ - ω₂ has an amplitude proportional to e₁² e₂ and will vary 2 db per decibel of signal-level change in e₁, and 1 db per decibel of change in e₂.

Thus, the power series defines the nonlinearity in terms of easily recognized frequency components, whose dependence on signal level can be readily determined.

Total harmonic distortion analysis requires only one signal source. Because of the system nonlinearity, simple harmonics of the input signal are generated at the output. The measurement technique compares the amplitude of the harmonics to that of the original signal at the output, where the original signal becomes the fundamental frequency of the harmonics. The defining equation is

A frequency-selective voltmeter is needed to measure the fundamental; and either a selective voltmeter with a wide dynamic range or a frequency rejection circuit with a true rms detector to measure the harmonics. The frequency rejection circuit nulls the fundamental and passes its harmonics to the detector with no attenuation, so the ratio between the fundamental and harmonics can be determined.

A less expensive way to measure the total harmonic distortion, however, is to use a rejection filter and a broadband detector. Since the fundamental is not directly measured, the equation becomes

If the distortion is less than 10%, the denominator of equation 2 will be within 1/2% of the denominator in equation 1, which is as accurate as any frequency selective voltmeter.

To cut costs further, most manufacturers use an averaging detector instead of a broadband detector. Under certain conditions, this can lead to reading errors in the null that are 20% to 30% low, since the averaging detector responds to the area of the rectified waveform and not to the instantaneous power of the wave shape. Even so, these types of errors are not considered significant; they affect only the over-all percentage of harmonics present in the output signal and not the individual terms, and the percentage is small. For example, a 20% error in reading the null of a system with 0.1% harmonics results in reading of 0.08% instead.

A more important error, much larger than the metering error, is caused by the attenuation of the harmonics by the rejection circuit. This error normally effects the second harmonics more than the higher ones. However, manufacturers of these circuits generally specify the second-harmonic attenuation, which makes it easy to compensate mathematically for the error in the readings.

There are two difficulties in making total harmonic distortion measurements. First, to get a measurement within the desired accuracy, the harmonic content of the test signal must be not more than a third of the distortion expected to be caused by the system. Second, the chore of nulling the fundamental can be time-consuming. Oscillators that meet the distortion requirements and automatic nulling equipment, which has recently become available, can overcome the difficulties.

The total harmonic method is very useful when testing low-distortion circuits, which require a large amount of negative feedback and must be unconditionally stable. It is important that oscillations that occur in these circuits be detected. In a TH system, the harmonics can be viewed on an oscilloscope, with the fundamental filtered out. Not only can the character of the distortion be easily determined, but residual oscillations that would have been much harder to find with a wave analyzer, and are too small in comparison to the fundamental to be detected on an oscilloscope, can be viewed.

In the CCIF method of distortion measurement, two signals are applied to the system under test. The diagram above shows how the low-pass filter separates the low-frequency intermodulation terms from these two signals. The amplitudes of the intermodulation, or difference terms, can be compared with that of the input signals. The lower frequency intermodulation terms are only even.

Two signals, f₁ and f₂, are used in the SMPTE method, with one having 50 times the frequency and one-quarter of the magnitude of the other. The frequencies of interest are restricted, as shown in the diagram, to a pass-band that is 20 times the higher frequency and centered around it. The envelope of these terms is then used to determine the modulation index of the higher frequency, f₂ in the above diagram.

Only the SMPTE method of intermodulation distortion measurement and the harmonic distortion technique measure both odd and even order nonlinearities. When used to analyze amplifiers, each method defined the non-linearities of the system in the same manner and gave the same information. They only differed by a scale factor.

There are three major methods of making intermodulation distortion measurements. In the Comité Consultatif International Téléphonique (CCIF) method, two high-frequency signals with amplitudes e₁ and e₂ are applied to the amplifier under test. The difference between their frequencies must lie within the amplifier's passband. The low-frequency difference products are extracted from the output signal with a low-pass filter, and their amplitudes are compared to those of the two original signals. If the input-signal amplitudes are equal to each other and represented by e/2, then

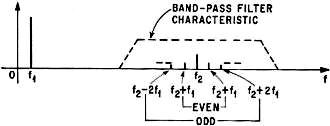
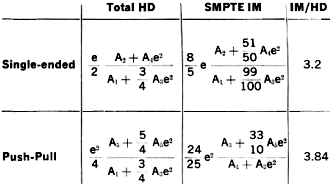
There is one serious fault with this method: only the even-order terms in the nonlinearity are detected. As a result, it is not a good method where the system distortion is expected to contain primarily odd-order terms, such as in a push-pull amplifier, or an amplifier that is overdriven.

Another method, used by the Society of Motion Picture and Television Engineers, also requires two input signals, one of which has 50 times the frequency and only one-fourth the amplitude of the other. The output is put through a band-pass filter, which filters out everything except the intermodulation terms. The latter are envelope-detected, and then low-pass filtered. The distortion is defined as the modulation index of the higher input frequency. With this method, both even- and odd-order non-linearities are detected. The response to the even ones are the sidebands corresponding to f₂ + (2n-1)f₁ and the response to the odd are the f₂² ± 2nf₁ sidebands. The bandwidth of the bandpass filter should be approximately 20 f₁ to ensure passing all the sidebands.

With the conditions that e₁/4 = e₂, the intermodulation distortion of a push-pull amplifier and a single-ended amplifier can be derived from the Taylor series. They are shown in the table at the top of this column.

A serious drawback of this technique is that the envelope detection process is nonlinear. If the signal amplitudes are low, as is often the case in transistor circuits, envelope detection can add significantly to the distortion at the output. Such circuits can be tested, however, if a wave analyzer - basically a selective voltmeter - replaces the envelope detector. This procedure requires tuning to and measuring all the spurious frequencies generated, and then computing the modulation index. The results are very reliable, but the procedure is time-consuming and the equipment is considerably more expensive than that used in the total harmonic distortion method. And since all spurious frequencies must be measured, the upper cutoff frequency of the system being tested must be 50 times greater than the lower cutoff frequency to pass all the significant frequencies.

In fact, all of the methods discussed so far work only with broadband systems. But there is one technique of intermodulation distortion measurement that is designed specifically for such limited passband systems as intermediate-frequency amplifiers. Again, two signals whose significant intermodulation products lie within the amplifier's passband are applied to the system. In this technique, if e₁ and e₂ = e/2 then

This method detects only the odd-order terms of nonlinearity, since the sum of the coefficients of the terms in the output closest to the test signal is odd. This method is quite satisfactory in the case of i-f amplifiers, because only the odd terms cause significant spurious responses. The equipment normally used is a wave or spectrum analyzer.

Two signals, close together, are used in the narrow band method of distortion analysis. The amplifier under test has a narrow pass-band, and the intermodulation terms measured are restricted to this band. As shown in the diagram above, these terms are all odd.

To obtain complete distortion data, it is necessary, in most cases, to detect both even and odd nonlinearities. Of the systems discussed, only total harmonic distortion analysis and the SMPTE intermodulation methods have this capability. A brief summary of a comparison between these two methods, made by W. J. Warren and W. R. Hewlett², is shown in the table on page 82. The ratios of intermodulation to harmonic distortion (IM/HD) shown will hold true for any frequency-independent system in a predictable manner. Both methods give the same information about the coefficients of the power series describing the amplifier; the answers just differ by a scale factor. Even so, intermodulation measurements are more difficult to make and generally require more sophisticated equipment than total harmonic measurements.

Intermodulation measuring requires two test signals which have no prior interaction. The distortion of these two signals does not have to be low, since their harmonics will not usually cause any significant intermodulation products. Setting up a measurement at one set of test frequencies is not difficult; but if measurements are required at several different sets of frequencies, the procedure becomes very complicated - especially if it is necessary to tune to each intermodulation term separately.

With the total harmonic distortion method however, both high and low frequency response can be easily measured, since only one signal frequency need be changed. This is useful when checking the effects of diminishing feedback gains at either end of the frequency response characteristic or the effect of load capacitance at the high-frequency end. In addition, the total harmonic distortion method requires only that the system have a flat frequency response over a frequency deviation of three to one, whereas the SMPTE method requires a flat response for a deviation greater than 50 to one.

Since the nulling of the fundamental is normally the time-consuming portion of total harmonic distortion measurement, great savings can be realized, especially in production line testing with an analyzer which automatically rejects the fundamental. The time saved is as much as 25 seconds of a 30-second measurement. With automatic nulling, the accuracy of the null achieved is no longer a function of operator training, manual dexterity or signal source frequency drift.

Automatic nulling circuitry in a new commercial wave analyzer, the H-P 333A and 334A, operates on the principle that the fundamental at either side of a Wien bridge off null follows well-known phase relationships. In this instrument, phase-sensitive feedback loops are employed which drive photo-cells in parallel with the resistances on either side of the bridge. These loops reject the fundamental and are not critical to adjust, since any imbalance on one side of the bridge is automatically compensated for on the other. Imbalances on either side cause phase errors in the fundamental which are in quadrature, so the phase-sensitive feedback loops are independent of each other.

The analyzer will maintain a null even though there is a slow drift in the input frequency. This ability to "pull" the null has opened the door to a number of applications where the total harmonic distortion measurements were not readily applied in the past. Among them are:

• Single-frequency production line testing of such components as integrated-circuit amplifiers or transformers. As long as the long-term drift of the signal source is less than ±1 %, a good null will always be achieved. Therefore, time-consuming rebalancing operations at the test position are eliminated.

• Optimizing the performance of an oscillator. Here, any variation in the parameters causes the frequency to shift slightly. The automatic nulling of the analyzer allows the oscillator performance to be improved on a continuous basis, rather than by relying on a point-to-point check, which may or may not find the optimum point.

• Correcting distortion in signal generators which produce sine waves either by mixing or by non-linear shaping. The small frequency shifts that occur in the process would also cause the loss of the null if it were not for the automatic null feature.

1. B.M. Oliver, "Distortion and intermodulation," Hewlett-Packard Co., Application note 15.

2. W.J. Warren and W.R. Hewlett, "Analysis of intermodulation method of distortion measurement," Proceedings of the IRE, p. 457-466, April, 1948.

Charles R. Moore is a group leader at the research and development laboratories of the Hewlett-Packard Company's Loveland division. He is a graduate of Princeton University and earned his master's degree in electrical engineering at the University of California.

Two Ways to Measure DistortionOctober 4, 1965 Electronics Magazine

Two Ways to Measure Distortion
October 4, 1965 Electronics Magazine