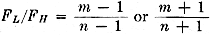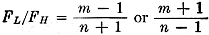Linear Scales Show Mixer Harmonics
January 10, 1964 Electronics Magazine

January 10, 1964 Electronics [Table of Contents] Wax nostalgic about and learn from the history of early electronics. See articles from Electronics, published 1930 - 1988. All copyrights hereby acknowledged.

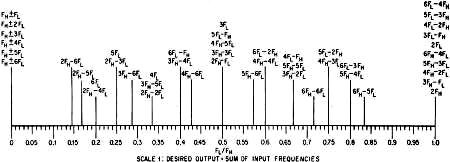
Having been out of the RF system design realm for a few years, I do not have much cause to think about mixer spurious products anymore. This "Linear Scales Show Mixer Harmonics" article from a 1964 issue of Electronics magazine got me thinking about it. I wonder these days how many designers even do much in the way of frequency planning in conversion systems? Are the RF, IF, and baseband frequencies so well defined for most of what is done in the wireless world that all the spurious product issues have been solved and there are few people who need to calculate mixer spurious product frequencies and powers? If there is a need, what methods are currently being used? Do you still cobble together spreadsheets and/or MATLAB worksheets using equations like those presented here, do you have a favorite smartphone app, a compact program on your computer, or are you using one of the two or three uber-sophisticated and super expensive design engineering programs like those sold by NI-AWR (MWO) and Keysight (ADS)? This inquiring mind wants to know.

Linear Scales Show Mixer Harmonics

Simplified method locates spurious signals generated by the first six harmonics of two mixed signals: one scale is for the sum, the other for the difference, of input frequencies

By Roger T. Stevens, Sanders Associates, Inc., Nashua, N. H.

When two r-f signals are mixed to produce a sum or difference frequency output, the mixing is inherently a nonlinear process that produces harmonics of the two incoming signals, resulting in spurious outputs corresponding to these harmonics and the various combinations of their sums and differences. If the relation of the incoming signals and local oscillator frequencies is chosen unwisely, some of these spurious signals will be at the desired output frequency, so that they cannot be filtered out. In many cases, the resulting distortion of the i-f signal is intolerable.

Many charts and tables have been published that make it possible to determine where the spurious frequencies lie, but they all are so general and so complex that they do not substantially simplify the task of the design engineer. The two linear scales shown here quickly and easily locate and identify all of the spurious signals generated by the first six harmonics of the two incoming signals. One scale is for use when the desired output signal is the sum of the two input signals and the other scale is used when the output must be the difference of the two input signals. The only other information required is the ratio of the lower frequency input signal (F_L) to the higher frequency input signal (F_H). For example, an input signal of 88 to 108 Mc is mixed with a local oscillator of 98.7 to 118.7 Mc to produce a 10.7-Mc i-f signal. The ratio F_L/F_H varies between 0.893 and 0.911. Looking at scale 2 (since the desired output is the difference frequency) we see that no spurious signals occur over this range and, therefore, the choice of local oscillator and i-f frequencies was satisfactory.

Equations - The derivation of the equations for these spurious signals is simple. The relation for the case of a desired difference signal output is

± (mF_H - nF_L) = F_H - F_L

where m and n are integers representing the particular harmonics of the desired signal. This equation can be rewritten in terms of the frequency ratio F_L/F_H

To make up the scale, all combinations of the first six harmonics of each input were calculated, but solutions that gave F_L/F_H > 1 or negative were discarded since these cases are excluded by definition.

The corresponding equation for the case of the sum frequency being the desired output is

± (mF_H - nF_L) = F_H + F_L

This can be reduced to

The scale was calculated from this formula in the same way that the difference frequency scale was determined.

Reference Sheets

Scale 1: Desired Output = Sum of Input Frequencies

Scale 2: Desired Output = Difference of Input Frequencies

Posted October 27, 2023
(updated from original post on 11/15/2018)