Undersampling of Modulated Signals |
|
According to the Nyquist sampling theorem, in order to recover a signal via sampling, the sample rate must be
greater than or equal to the two time (2x) the highest frequency in the signal. Doing so prevents aliasing due to
frequency foldback about the 0 Hz (DC) axis. So, if you were digitally sampling a human voice with a maximum
frequency content of, say, 6 kHz, then your sampling rate would need to be at least 12 kHz. In practice, the
sample rate used is a little higher to provide a buffer, and a lowpass filter is placed in front of the A-to-D
converter to make certain that higher frequency content does not make its way into the converter and subsequently
get translated into an aliased (false) component. The concept applies to digital signals as well as with analog
signals. In the case of a higher frequency carrier onto which lower frequency information is modulated, it is necessary to translate the information content down to a frequency band low enough for the A-to-D converter (ADC) to use. Modern (as of 2006) ADCs easily operate at sample rates beyond 100 MHz while delivering 12 to 14 bits or more of resolution. That is a phenomenal achievement considering that a mere 15 years ago radar design teams I worked on were struggling to do 10-12 bits at 20 MHz using custom-designed circuits. If you had an ADC running at 216 MHz, it would be possible to directly sample the FM radio band signal (88 - 108 MHz) and demodulate the information in software. We're not quite there yet, so it is still necessary to use and RF mixer to downconvert the RF to a baseband frequency that can be used. AM radio (520 – 1,610 kHz) could, though, be directly sampled at RF. There is another option called undersampling (sometimes called bandpass sampling, or super-Nyquist sampling) whereby the aliasing phenomenon is exploited to enable the ADC to sample the signal using a rate that intentionally aliases the modulated carrier (fCARRIER) into the operating range of the ADC. Determining the necessary sampling frequency (fSAMPLE), is a fairly simple 2-step process that uses the following two formulas:
(eq. 1)
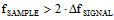 (eq. 2) (eq. 2) 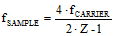 As an example, consider a 20 MHz signal modulated on a 2 GHz carrier. Per the Nyquist sampling theorem, a clock rate of at least 4.04 GHz (2 x 2.02 MHz) would be needed to directly sample this signal. Now, working through the above equations, we first solve equation 1 for the minimum sampling frequency: 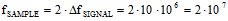 Next, plug that value into equation 2 to calculate Z, and round the answer down to the nearest integer value: 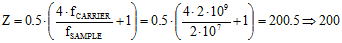 Finally, use the final value of Z to calculate the Undersampling frequency: 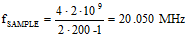 |