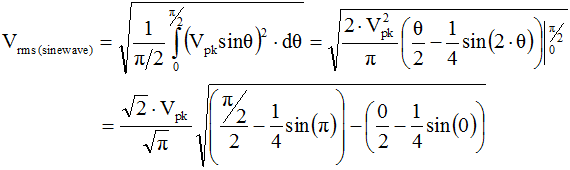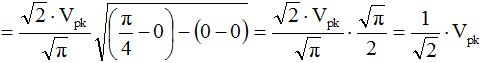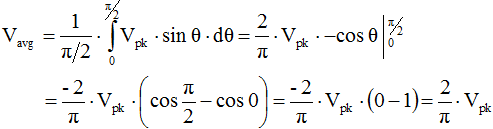Sinewave Voltages - Vpk, Vpk-pk, Vavg, Vrms |
|
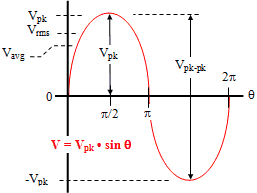
A sinewave is defined by the trigonometric sine function. When plotted as voltage (V) as a function of phase (θ), it looks similar to the figure to the right. The waveform repeats every 2p radians (360°), and is symmetrical about the voltage axis (when no DC offset is present). Voltage and current exhibiting cyclic behavior is referred to as alternating; i.e., alternating current (AC). One full cycle is shown here. The basic equation for a sinewave is as follows:
There are a number of ways in which the amplitude of a sinewave is referenced, usually as peak voltage (Vpk or Vp), peak-to-peak voltage (Vpp or Vp-p or Vpkpk or Vpk-pk), average voltage (Vav or Vavg), and root-mean-square voltage (Vrms). Peak voltage and peak-to-peak voltage are apparent by looking at the above plot. Root-mean-square and average voltage are not so apparent. Also see Triangle Wave Voltages and Square Wave Voltages pages. Root-Mean-Square Voltage (Vrms)
Vrms is the value indicated by the vast majority of AC voltmeters. It is the value that, when applied across a resistance, produces that same amount of heat that a direct current (DC) voltage of the same magnitude would produce. For example, 1 V applied across a 1 Ω resistor produces 1 W of heat. A 1 Vrms sinewave applied across a 1 Ω resistor also produces 1 W of heat. That 1 Vrms sinewave has a peak voltage of √2 V (≈1.414 V), and a peak-to-peak voltage of 2√2 V (≈2.828 V). Since finding a full derivation of the formulas for root-mean-square (Vrms) voltage is difficult, it is done here for you.
So, 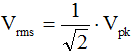 ≈ 0.707 Vpk, where
≈ 0.707 Vpk, where
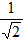 = 0.70710678118654752440084436210485
= 0.70710678118654752440084436210485
Average Voltage (Vavg) As the name implies, Vavg is calculated by taking the average of the voltage in an appropriately chosen interval. In the case of symmetrical waveforms like the sinewave, a quarter cycle faithfully represents all four quarter cycles of the waveform. Therefore, it is acceptable to choose the first quarter cycle, which goes from 0 radians (0°) through p/2 radians (90°). As with the Vrms formula, a full derivation for the Vavg formula is given here as well.
So, 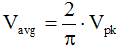 ≈ 0.636 Vpk, where
≈ 0.636 Vpk, where
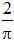 = 0.63661977236758134307553505349006
= 0.63661977236758134307553505349006
* I have no idea why we write "Sinewave," but not "Trianglewave" and "Squarewave." |
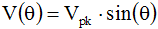
 As
the name implies, Vrms is calculated by taking the square root of the mean average of the square of the
voltage in an appropriately chosen interval. In the case of symmetrical waveforms like the sinewave, a quarter cycle
faithfully represents all four quarter cycles of the waveform. Therefore, it is acceptable to choose the first quarter
cycle, which goes from 0 radians (0°) through
As
the name implies, Vrms is calculated by taking the square root of the mean average of the square of the
voltage in an appropriately chosen interval. In the case of symmetrical waveforms like the sinewave, a quarter cycle
faithfully represents all four quarter cycles of the waveform. Therefore, it is acceptable to choose the first quarter
cycle, which goes from 0 radians (0°) through