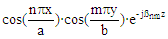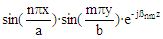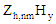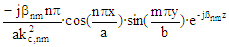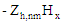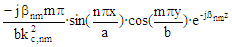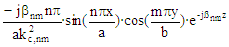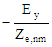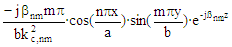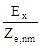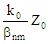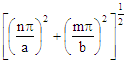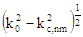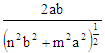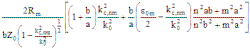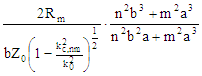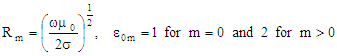Electronics World articles Popular Electronics articles QST articles Radio & TV News articles Radio-Craft articles Radio-Electronics articles Short Wave Craft articles Wireless World articles Google Search of RF Cafe website Sitemap Electronics Equations Mathematics Equations Equations physics Manufacturers & distributors Engineer Jobs LinkedIn Crosswords Engineering Humor Kirt's Cogitations Engineering Event Calendar RF Engineering Quizzes USAF radar shop Notable Quotes App Notes Calculators Education Engineering Magazines Engineering magazine articles Engineering software Engineering smorgasbord RF Cafe Archives RF Cascade Workbook 2018 RF Stencils for Visio RF & EE Shapes for Word Advertising RF Cafe Homepage Sudoku puzzles Thank you for visiting RF Cafe!
MECA Electronics

Properties of Modes in a Rectangular Waveguide
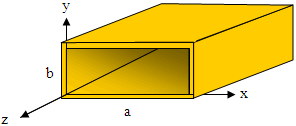
Rectangular waveguides, as opposed to circular and elliptical waveguides, are by far the dominant configuration for the installed base of waveguides for compact systems like radar and inside equipment shelters. That is probably due to the generally greater rigidity of rectangular structures because the wall thickness can be easily made thicker than with circular. It is also easier to route and mount in close quarters, and attaching penetrating objects like probes and switches is much simpler.

Rectangular waveguide variables - RF Cafe


Tabel of Time-Harmonic Mode Properties in a Rectangular Waveguide, by Brian Sequeira - RF CafeMost rectangular waveguide calculations can be performed on any calculator that has trig function keys. Calculations for circular waveguide, on the other hand, requires the application of Bessel functions, so working equations with a cheap calculator is not going to happen. However, even spreadsheets have Bessel function capability nowadays, so determining cutoff frequencies, field strengths, and any of the other standard values associated with circular waveguide can be done relatively easily. The formulas below represent those quantities most commonly needed for rectangular waveguides. Please see the figure at the right for variable references.

Note: I received the following note from Brian Sequeira, of the Johns Hopkins University Applied Physics Laboratory. "I reviewed tables on rectangular and circular waveguides, and based on my experience of what confuses first-time readers and what does not, I made adjustments to notation & symbols, corrected a couple of sign errors, and put expressions in a form that make their units more apparent." The table for rectangular waveguide can be viewed full-size by clicking on the thumbnail to the right. Brian also provided a table for circular waveguide.
 
Quantity TE Modes TM Modes
Hz Rectangular waveguide mode equations - RF Cafe 0
Ez 0 Rectangular waveguide mode equations - RF Cafe
Ex Rectangular waveguide mode equations - RF Cafe Rectangular waveguide mode equations - RF Cafe
Ey Rectangular waveguide mode equations - RF Cafe Rectangular waveguide mode equations - RF Cafe
Hx Rectangular waveguide mode equations - RF Cafe Rectangular waveguide mode equations - RF Cafe
Hy Rectangular waveguide mode equations - RF Cafe Rectangular waveguide mode equations - RF Cafe
Zh,nm Rectangular waveguide mode equations - RF Cafe  
Ze,nm   Rectangular waveguide mode equations - RF Cafe
kc,nm   Rectangular waveguide mode equations - RF Cafe
βnm   Rectangular waveguide mode equations - RF Cafe
λc,nm   Rectangular waveguide mode equations - RF Cafe
α† Rectangular waveguide mode equations Rectangular waveguide mode equations - RF Cafe
† Rectangular waveguide mode equations - RF Cafe

The expression for α is not valid for degenerate modes.
Equations derived from "Foundations for Microwave Engineering, R.E. Collin, McGraw-Hill

Related Pages on RF Cafe

- Properties of Modes in a Rectangular Waveguide
- Properties of Modes in a Circular Waveguide
- Waveguide & Flange Selection Guide
- Rectangular & Circular Waveguide: Equations & Fields
- Rectangular waveguide TE1,0 cutoff frequency calculator.
- Waveguide Component Vendors
- NEETS - Waveguide Theory and Application
- EWHBK, Microwave Waveguide and Coaxial Cable


Windfreak Technologies ConductRF Phased Matched RF Cables - RF Cafe
NorthEast RF Antenna Testing Services Berkeley Nucleonics Academy - RF Cafe
About RF Cafe
Kirt Blattenberger - RF Cafe Webmaster
Copyright: 1996 - 2024
Webmaster:
    Kirt Blattenberger,
    BSEE - KB3UON

RF Cafe began life in 1996 as "RF Tools" in an AOL screen name web space totaling 2 MB. Its primary purpose was to provide me with ready access to commonly needed formulas and reference material while performing my work as an RF system and circuit design engineer. The World Wide Web (Internet) was largely an unknown entity at the time and bandwidth was a scarce commodity. Dial-up modems blazed along at 14.4 kbps while typing up your telephone line, and a nice lady's voice announced "You've Got Mail" when a new message arrived...

All trademarks, copyrights, patents, and other rights of ownership to images and text used on the RF Cafe website are hereby acknowledged.

My Hobby Website:  AirplanesAndRockets.com

spacer

Please Support RF Cafe by purchasing my  ridiculously low−priced products, all of which I created.

These Are Available for Free