Norton Equivalent Circuit Theorem |
||||
|
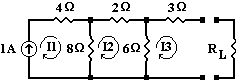
Norton's theorem for electrical networks states that any collection of voltage sources, current sources, and
resistors with two terminals is electrically equivalent to an ideal current source, I, in parallel with a single
resistor, R. For single-frequency AC systems the theorem can also be applied to general impedances, not just
resistors. The Norton equivalent is used to represent any network of linear sources and impedances, at a given
frequency. The circuit consists of an ideal current source in parallel with an ideal impedance (or resistor for
non-reactive circuits).
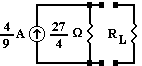
- Wikipedia The Norton Equivalent of a circuit consists of a Norton current source in parallel with a Norton resistor and is valid for any load. In AC circuits a Norton equivalent circuit is valid for a single frequency. The Norton current is the short-circuit current at the output - the same as what is calculated for the Thévénin short-circuit current (see Thévénin Equivalent page). The Norton resistance is the same as the Thévénin resistance.
|
||||