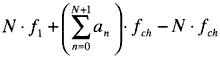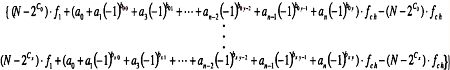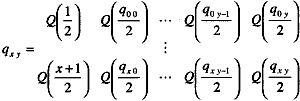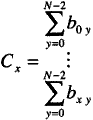A General Algorithm to Calculate Third Order Intermodulation Product
- Locations for any Number of Tones -

 by Chris Arnott

A web exclusive from CED Magazine

Note: This paper used to be available on the CED (Communications Engineering & Design) website, but has been removed. So, I scanned the copy provided to me by the author, Chris Arnott, when we worked together at RFMD. I will remove the article at the request of CED.

Cable operators offering digital communication services on their systems provide customers with Internet access, digital video and business network solutions to add flexibility and profitability to their systems. A major system consideration for successful implementation of a modem digital cable system is system linearity. Inadequate system linearity distorts the channel information and can lead to low system operability or reliability.

Amplifying components placed within the system for signal amplification or frequency conversation contribute to system distortion. All amplifiers and frequency conversion components exhibit non-linear amplification and produce distortion, causing intermodulation products. This distortion corrupts the channels and can lead to high bit-error rates. The problem is more severe in these wideband cable systems because each amplifying component input sees the entire high-power multichannel cable system spectrum.

The number of distorting intermodulation products created by these inline-amplifying components is very large. Worse, many of these intermodulation products fall within the same channels and the distortion power accumulates with the number of products. This accumulated distorting power is the main reason why poor system linearity can cause low system reliability. Therefore, care must be taken when selecting amplification components for wideband cable systems in order to ensure adequate system linearity.

This paper shows a general algorithm to calculate the number of distortion products created by a third-order non-linearity in a wideband multichannel system.

This article describes a general algorithm to calculate the frequency locations of third-order intermodulation distortion products produced by a broadband amplifier for any number of test tones. It also defines a broadband system with equally spaced channels. The analysis includes a calculation of total primary and intermodulation product signals produced by non-linear third-order systems and a discussion of where the most important intermodulation distortion products lay. A practical example of a four-tone test is then performed on a standard IRC cable TV system with third-order non-linearity.

on-linearity of amplifiers in broadband applications greatly contributes to system performance degradation because of interfering distortion signals. Broadband systems containing many equal-power channels produce intermodulation distortion signals when amplified by line amplifiers and LNAs.

Narrowband systems readily use simple two-tone tests to analyze third-order intermodulation distortion [1]. Narrowband intermodulation analysis is simplified by ignoring distortion products not located within close proximity of the desired channel. These simplifications cannot be readily utilized in broadband system intermodulation distortion analysis many intermodulation products lie within the system bandwidth. Intermodulation distortion analysis is more difficult in broadband systems because all intermodulation products can interfere with many channels simultaneously Therefore, broadband systems require multi-tone tests to analyze third-order intermodulation distortion.

Third-Order Broadband System Distortion Analysis

Broadband systems are comprised of many equally spaced channels.

A broadband system with equally spaced multi-channels is described by equation 1,

f_i = f₁ + (i -1) · f_ch   for i = 1,2,3,···, N + 1      Eq. 1

where i represents the channel number, f1 represents the beginning channel frequency, represents the number of channels, and fch represents the channel spacing. A non-linear third-order distorting amplifier produces four types of tones: the primary; the third harmonic; the third-order intermodulation products; and frequency sum products.

The terminology, "third-order intermodulation product" is traditionally used to define the important intermodulation products in narrowband analysis. This terminology, though technically incorrect, is used to define the same products in broadband intermodulation analysis and will be clarified later. The third harmonic, third-order products, and frequency sum products are interference signals that degrade desired channel reception. The amplifier passes all N primary tones and generates a total of N third harmonic distortion tones. The number of third-order intermodulation distortion products produced by the amplifier is given by equation 2.

N_3rd = 2 · N · (N -1)   for N ≥ 2      Eq. 2

The number of frequency sum distortion products generated by the amplifier is given by equation 3.

N_sum = 2^N-1   for N ≥ 2       Eq.3

Combining the number of primary and third harmonic tones and equations 2 and 3, the total number of tones at the amplifier's output is given by equation 4.

N_TOT = 2 · N + 2 · N ·(N-1) + 2^N-1   for N ≥ 2      Eq.4

The total number of output tones increases dramatically as the number of channels increases, which indicates the importance of good system linearity because each distortion tone can potentially distort a channel. The frequency sum products are the largest number and strongest interfering distortion products and contribute more to desired signal degradation [23]. The power frequency sum distortion products are 6 dB higher than the third-order products [3]. The higher power and greater number is the reason the frequency sum products are considered the most important.

The frequency location of intermodulation distortion interferers in a broadband system with third-order non-linearity is investigated by applying N arbitrary channel frequency tones. Each tone is assumed to be of equal amplitude and have zero degree correlated phase. The N tones in an arbitrarily spaced N-channel system are defined using equation 1 as

f_a0 = f₁ + (a₀ - 1) · f_ch                 

f_an = f₁ + (a_n -1) · f_ch       Eq.5

where an is a positive non-zero successively increasing sequence of integers given by

Using a composite input signal formed by a summation of cosine functions with frequencies a broadband system intermodulation analysis can be performed. The non-linear amplifier is simulated as a third degree monomial with a coefficient of one or gain of one. Cubing the composite function and using trigonometric identities the frequency locations of the output tones are found as four distinct sequences as given by, for the primary tones (see equation 7)

for the third harmonic tones (see equation 8),

and third-order intermodulation products (see equation 9),

The definition of the third-order intermodulation given in equation 9 is the same as for tones used to describe intermodulation distortion in narrowband analysis. Three sequences describe the frequency sum products. The first and last sum products are unique where the first product location is given by equation 10,

      Eq.10

and the last term is located at (see equation 11),

      Eq. 11

The sequence for the frequency locations of the remaining sum products is given by (see equation 12),

      Eq.12

where

x = 0, 1, 2, · · ·, 2^N-1 - 1, 2^N-1 - 2, 2^N-1 - 3,      Eq. 13

and

y = 0, 1, 2, · · ·, N - 4, N - 3, N - 2       Eq.14

Exponent bxy is an element in Bxy that describes the base 2 binary digits of x + 1 for each x state with N -1 significant bits and Cx is the sum of the binary digits represented by row elements bxy. The sequence described in (12) locates the sum product frequency locations by negating coefficients a1 - an for all possible x states. Matrix Bxy ~d vector Cx are found with numerical base 2 conversion techniques. First a calculation of an x by y matrix containing the quotients of state x divided by 2 in column 0 is given by equation 15.

      Eq.15

The x by y matrix Bxy contains elements with the remainders of state x+ 1 divided by 2 in column 0 is given by equation 16,

      Eq.16

where the row elements represent base 2 binary digits of x+ 1 to N-l significant bits. The vector Cx is the summation of the row elements of Bxy as given by equation 17

      Eq.17

As an example, a system exhibiting third-order non-linearity is subjected to a four-tone test using equations 5 through 17. The four equally spaced tones are defined using equation 5 as

f_a0 = f₁ + (a₀ - 1) · f_ch      Eq. 18

f_a1 = f₁ + (a₁ - 1) · f_ch

Eq.19

f_a2 = f₁ + (a₂ - 1) · f_ch      Eq. 20

and

f_a3 = f₁ + (a₃ - 1) · f_ch      Eq.21

A total of 40 tones are generated by the non-linear system: four primary tones; four third-harmonic tones; 24 third-order intermodulation products (from equation 2); and eight frequency sum products (from equation 3). The primary tones, third-harmonic and third-order intermodulation tones using equations 7, 8 and 9 are given by

{f_a0, f_a1, f_a2, f_a3}            Eq.22

{3 · f_a0, 3 · f_a1, 3 · f_a2, 3 · f_a3}       Eq.23

and

{2 · f_a0 ± f_a1, 2 · f_a0 ± f_a2, 2 · f_a0 ± f_a3,              

  2 · f_a1 ± f_a0, 2 · f_a1 ± f_a2, 2 · f_a1 ± f_a3,              

  2 · f_a3 ± f_a0, 2 · f_a3 ± f_a1, 2 · f_a3 ± f_a2, }       Eq.24

The sum product frequency locations for the four-tone test are found using equations 10 through 17. The first and last frequency sum product using equations 10 and 11 are given by

4 · f₁ + (a₀ + a₁ + a₂ + a₃) · f_ch - 4 · f_ch        Eq.25

and

2 · f₁ + (a₃ + a₂ + a₁ - a₀) · f_ch - 2 · f_ch       Eq.26

The first step in finding the remaining sum product frequency locations is calculating matrices qxy and Bxy with x and y having six states and three significant bits. Using equation 15, qxy and Bxy are given by

Eq.27

and

Eq.28

Using equation 17, the vector Cx is given by

C_x =1  1  2  1  2  2        Eq.29

Knowing bxy and Cx the remaining sum product frequency location sequence using equation 12 is given by

{2 · f₁ + (a₀ - a₁ + a₂ + a₃) · f_ch - 2 · f_ch

  2 · f₁ + (a₀ + a₁ - a₂ + a₃) · f_ch - 2 · f_ch

  (a₀ - a₁ - a₂ + a₃) · f_ch

  2 · f₁ + (a₀ + a₁ + a₂ - a₃) · f_ch - 2 · f_ch

  (a₀ - a₁ + a₂ - a₃) · f_ch

                    (a₀ + a₁ - a₂ - a₃) · f_ch  }      Eq.30

An investigation of the frequency sum distortion products in a real broadband system is investigated by applying four arbitrary, successively increasing frequency tones to a system with third-order non-linearity. The tones are assumed to have equal amplitude and a correlated phase of zero degrees. Phase correlation between the test tones causes correlation between the intermodulation products. This correlation between the intermodulation products causes products falling on the same channel to add as voltages and is considered worst case. Each intermodulation product falls within close proximity to a channel in systems with no correlation between tones and appears like a noise signal. This noise like signal is the sum root mean square power of each distortion product and causes less distortion compared to a correlated system.

The beginning channel frequency fl is chosen as 121.25 MHz, standard IRC cable TV video carrier frequency with 6 MHz carrier spacing. The fourth tone is 18 MHz greater than fl. The bandwidth of the system for investigation of the distortion products is 624 MHz. Tones a0 - a3 are chosen as four successively increasing frequencies for cases a0 equal 1 through 10.

A result of (30) for an even number of tones is constant distortion product frequencies for products with an equal number of positive and negative an coefficients. These constant product frequencies can be ignored because they do not lie above the beginning channel. The frequency locations of the non-constant frequency sum distortion products are shown in table 1. Each distortion sum product in table 1 lies within a channel in a typical cable TV system, and will interfere with desired channels.

Interestingly, the frequency sum products in the last four columns fall in at the same frequency as second-order intermodulation (composite second order) products at +1.25 MHz offset form the carrier. This indicates a system with four much higher power carriers relative to the remaining carriers can produce third-order products that appear as second-order products.

Conclusion

Results show that broadband intermodulation distortion analysis cannot utilize assumptions used in narrowband system analysis. The ignored frequency sum products in narrowband analysis can distort channels in broadband systems. Results of equation 3 show the number of interfering sum products greatly increase as the number of channels increase in a broadband system with third-order non-linearity. The algorithm correctly calculates the distortion product frequency locations for the general case of any number of test tones.

Acknowledgements

The author thanks Dr. Bruce Schmukler, Greg Schramm, and Jennifer Ameling of RF Micro Devices for many useful comments and discussions related to this article.

References

  [1] T. H. Lee, The Design of CMOS Radio-Frequency Integrated Circuits. Cambridge, U.K.: Cambridge Univ. Press 1998.

  [2] Some Notes on Composite Second and Third Order Intermodulation Distortions, Matrix Technical Notes MT -108, Matrix Test Incorporated, 12/1998

  [3] The Relationship of Intercept Points and Composite Distortions,

Matrix Technical Notes MTN-109, Matrix Test Inc., 2/1998

 -- Chris Arnott

Posted May 7, 2024
(updated from original post on 8/1/2005)