Introduction to Electrical Conductors, Wiring Techniques, and Schematic Reading

NEETS Module 4 − Introduction to Electrical Conductors, Wiring Techniques, and Schematic Reading

Pages i, 1−1, 1−11, 1−21, 2−1, 2−11, 2−21, 2−31, 2−41, 3−1, 3−11, 3−21, 4−1, 4−11, Index

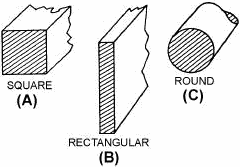
Learning objectives are stated at the beginning of each chapter. These learning objectives serve as a preview of the information you are expected to learn in the chapter. The comprehensive check questions are based on the objectives. By successfully completing the OCC-ECC, you indicate that you have met the objectives and have learned the information. The learning objectives are listed below.

1. Recall the definitions of unit size, mil-foot, square mil, and circular mil and the mathematical equations and calculations for each.

2. Define specific resistance and recall the three factors used to calculate it in ohms.

3. Describe the proper use of the American Wire Gauge when making wire measurements.

6. Define insulation resistance and dielectric strength including how the dielectric strength of an insulator is determined.

7. Identify the safety precautions to be taken when working with insulating materials.

In the previous modules of this training series, you have learned about various circuit components. These components provide the majority of the operating characteristics of any electrical circuit. They are useless, however, if they are not connected together. Conductors are the means used to tie these components together.

Many factors determine the type of electrical conductor used to connect components. Some of these factors are the physical size of the conductor, its composition, and its electrical characteristics. Other factors that can determine the choice of a conductor are the weight, the cost, and the environment where the conductor will be used.

To compare the resistance and size of one conductor with that of another, we need to establish a standard or unit size. a convenient unit of measurement of the diameter of a conductor is the mil (0.001, or one-thousandth of an inch). a convenient unit of conductor length is the foot. The standard unit of size in most cases is the MIL-FOOT. a wire will have a unit size if it has a diameter of 1 mil and a length of 1 foot.

The square mil is a unit of measurement used to determine the cross-sectional area of a square or rectangular conductor (views a and B of figure 1-1). a square mil is defined as the area of a square, the sides of which are each 1 mil. To obtain the cross-sectional area of a square conductor, multiply the dimension of any side of the square by itself. For example, assume that you have a square conductor with a side dimension of 3 mils. Multiply 3 mils by itself (3 mils x 3 mils). This gives you a cross-sectional area of 9 square mils.

Q2. Calculate the diameter in MILS of a conductor that has a diameter of 0.375 inch.

Cross-sectional areas of conductors - RF Cafe

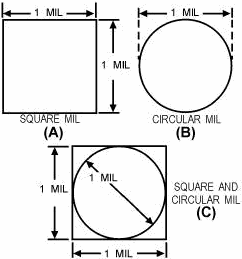
Figure 1-1. - Cross-sectional areas of conductors.

To determine the cross-sectional area of a rectangular conductor, multiply the length times the width of the end face of the conductor (side is expressed in mils). For example, assume that one side of the rectangular cross-sectional area is 6 mils and the other side is 3 mils. Multiply 6 mils x 3 mils, which equals 18 square mils. Here is another example. Assume that a conductor is 3/8 inch thick and 4 inches wide. The 3/8 inch can be expressed in decimal form as 0.375 inch. Since 1 mil equals 0.001 inch, the thickness of the conductor will be 0.001 x 0.375, or 375 mils. Since the width is 4 inches and there are 1,000 mils per inch, the width will be 4 x 1,000, or 4,000 mils. To determine the cross-sectional area, multiply the length by the width; or 375 mils x 4,000 mils. The area will be 1,500,000 square mils.

The circular mil is the standard unit of measurement of a round wire cross-sectional area (view C of figure 1-1). This unit of measurement is found in American and English wire tables. The diameter of a round conductor (wire) used to conduct electricity may be only a fraction of an inch. Therefore, it is convenient to express this diameter in mils to avoid using decimals. For example, the diameter of a wire is expressed as 25 mils instead of 0.025 inch. a circular mil is the area of a circle having a diameter of 1 mil, as shown in view B of figure 1-2. The area in circular mils of a round conductor is obtained by squaring the diameter, measured in mils. Thus, a wire having a diameter of 25 mils has an area of 25², or 625 circular mils. To determine the number of square mils in the same conductor, apply the conventional formula for determining the area of a circle (A = πr²). In this formula, a (area) is the unknown and is equal to the cross-sectional area in square mils, p is the constant 3.14, and r is the radius of the circle, or half the diameter (D). Through substitution, a = 3.14, and (12.5)²; therefore, 3.14 x 156.25 = 490.625 square mils. The cross-sectional area of the wire has 625 circular mils but only 490.625 square mils. Therefore, a circular mil represents a smaller unit of area than the square mil.

A comparison of circular and square mils - RF Cafe

Figure 1-2. - a comparison of circular and square mils.

If a wire has a cross-sectional diameter of 1 mil, by definition, the circular mil area (CMA) is a = D², or a = 1², or a = 1 circular mil. To determine the square mil area of the same wire, apply the formula A = πr²; therefore, a = 3.14 x (.5)² (.5 representing half the diameter). When a = 3.14 x .25, a = .7854 square mil. From this, it can be concluded that 1 circular mil is equal to. 7854 square mil. This becomes important when square (view a of figure 1-2) and round (view B) conductors are compared as in view C of figure 1-2.

When the square mil area is given, divide the area by 0.7854 to determine the circular mil area, or CMA. When the CMA is given, multiply the area by 0.7854 to determine the square mil area. For example,

Problem: a 12-gauge wire has a diameter of 80.81 mils. What is (1) its area in circular mils and (2) its area in square mils?

Problem: a rectangular conductor is 1.5 inches wide and 0.25 inch thick. What is (1) its area in square mils and (2) in circular mils? What size of round conductor is necessary to carry the same current as the rectangular bar?

(2) To carry the same current, the cross-sectional area of the round conductor must be equal.

A wire in its usual form is a single slender rod or filament of drawn metal. In large sizes, wire becomes difficult to handle. To increase its flexibility, it is stranded. Strands are usually single wires twisted together in sufficient numbers to make up the necessary cross-sectional area of the cable. The total area of stranded wire in circular mils is determined by multiplying the area in circular mils of one strand by the number of strands in the cable.

Q6. What is the circular mil area of a 19-strand conductor if each strand is 0.004 inch?

Circular-mil-foot - RF Cafe

Figure 1-3. - Circular-mil-foot.

A circular-mil-foot (figure 1-3) is a unit of volume. It is a unit conductor 1 foot in length and has a cross-sectional area of 1 circular mil. Because it is a unit conductor, the circular-mil-foot is useful in making comparisons between wires consisting of different metals. For example, a basis of comparison of the RESISTIVITY (to be discussed shortly) of various substances may be made by determining the resistance of a circular-mil-foot of each of the substances.

In working with square or rectangular conductors, such as ammeter shunts and bus bars, you may sometimes find it more convenient to use a different unit volume. a bus bar is a heavy copper strap or bar used to connect several circuits together. Bus bars are used when a large current capacity is required. Unit volume may be measured as the centimeter cube. Specific resistance, therefore, becomes the resistance

offered by a cube-shaped conductor 1centimeter in length and 1 square centimeter in cross-sectional area. The unit of volume to be used is given in tables of specific resistances.

Specific resistance, or resistivity, is the resistance in ohms offered by a unit volume (the circular-mil- foot or the centimeter cube) of a substance to the flow of electric current. Resistivity is the reciprocal of conductivity. A substance that has a high resistivity will have a low conductivity, and vice versa. Thus, the specific resistance of a substance is the resistance of a unit volume of that substance.

Specific Resistances of Common Substances - RF Cafe

Table 1-1. - Specific Resistances of Common Substances

Many tables of specific resistance are based on the resistance in ohms of a volume of a substance 1 foot in length and 1 circular mil in cross-sectional area. The temperature at which the resistance measurement is made is also specified. If you know the kind of metal a conductor is made of, you can obtain the specific resistance of the metal from a table. The specific resistances of some common substances are given in table 1-1.

The resistance of a conductor of a uniform cross section varies directly as the product of the length and the specific resistance of the conductor, and inversely as the cross-sectional area of the conductor. Therefore, you can calculate the resistance of a conductor if you know the length, cross-sectional area, and specific resistance of the substance. Expressed as an equation, the "R" (resistance in ohms) of a conductor is

What is the resistance of 1,000 feet of copper wire having a cross-sectional area of 10,400 circular

The specific resistance of copper (table 1-1) is 10.37 ohms. Substituting the known values in the

If R, ρ, and a are known, the length (L) can be determined by a simple mathematical transposition. This has many valuable applications. For example, when locating a ground in a telephone line, you will use special test equipment. This equipment operates on the principle that the resistance of a line varies directly with its length. Thus, the distance between the test point and a fault can be computed accurately.

Q8. List the three factors used to calculate resistance of a particular conductor in ohms.

The most common method for measuring wire size in the Navy is by using the American Wire Gauge (AWG). An exception is aircraft wiring, which varies slightly in size and flexibility from AWG standards. For information concerning aircraft wire sizes, refer to the proper publications for specific aircraft. Only AWG wire sizes are used in the following discussion.

Table 1-2. - Standard Solid Copper (American Wire Gauge)

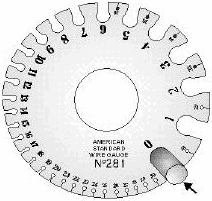
Wire gauge - RF Cafe

Figure 1-4. - Wire gauge.

Conductors - RF Cafe

Figure 1-5. - Conductors.

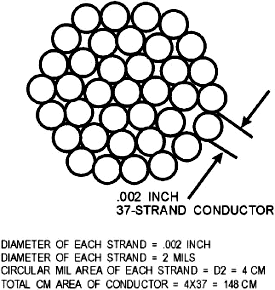
Stranded conductor - RF Cafe

Figure 1-6. - Stranded conductor.

Wire is manufactured in sizes numbered according to the AWG tables. The various wires (solid or stranded) and the material they are made from (copper, aluminum, and so forth) are published by the National Bureau of Standards. An AWG table for copper wire is shown at table 1-2. The wire diameters become smaller as the gauge numbers become larger. Numbers are rounded off for convenience but are accurate for practical application. The largest wire size shown in the table is 0000 (read "4 naught"), and the smallest is number 40. Larger and smaller sizes are manufactured, but are not commonly used by the Navy. AWG tables show the diameter in mils, circular mil area, and area in square inches of AWG wire sizes. They also show the resistance (ohms) per thousand feet and per mile of wire sizes at specific temperatures. The last column shows the weight of the wire per thousand feet. An example of the use of table 1-2 is as follows.

Problem: You are required to run 2,000 feet of AWG 20 solid copper wire for a new piece of equipment. The temperature where the wire is to be run is 25º C (77º F). How much resistance will the wire offer to current flow?

Solution: Under the gauge number column, find size AWG 20. Now read across the columns until you reach the "ohms per 1,000 feet for 25º C (77º F)" column. You will find that the wire will offer 10.4 ohms of resistance to current flow. Since we are using 2,000 feet of wire, multiply by 2.

An American Standard Wire Gauge (figure 1-4) is used to measure wires ranging in size from number 0 to number 36. To use this gauge, insert the wire to be measured into the smallest slot that will just accommodate the bare wire. The gauge number on that slot indicates the wire size. The front part of the slot has parallel sides, and this is where the wire measurement is taken. It should not be confused with the larger semicircular opening at the rear of the slot. The rear opening simply permits the free movement of the wire all the way through the slot.

Q9. Using table 1-2, determine the resistance of 1,500 feet of AWG 20 wire at 25º C.

Q10. When using an American Standard Wire Gauge to determine the size of a wire, where should you place the wire in the gauge to get the correct measurement?

A wire is a single slender rod or filament of drawn metal. This definition restricts the term to what would ordinarily be understood as "solid wire." The word "slender" is used because the length of a wire is usually large when compared to its diameter. If a wire is covered with insulation, it is an insulated wire. Although the term "wire" properly refers to the metal, it also includes the insulation.

A stranded conductor is a conductor composed of a group of wires or of any combination of groups of wires. The wires in a stranded conductor are usually twisted together and not insulated from each other.

A cable is either a stranded conductor (single-conductor cable) or a combination of conductors insulated from one another (multiple-conductor cable). The term "cable" is a general one and usually applies only to the larger sizes of conductors. a small cable is more often called a stranded wire or cord (such as that used for an iron or a lamp cord). Cables may be bare or insulated. Insulated cables may be sheathed (covered) with lead, or protective armor. Figure 1-5 shows different types of wire and cable used in the Navy.

Conductors are stranded mainly to increase their flexibility. The wire strands in cables are arranged in the following order:

The first layer of strands around the center conductor is made up of six conductors. The second layer is made up of 12 additional conductors. The third layer is made up of 18 additional conductors, and so on. Thus, standard cables are composed of 7, 19, and 37 strands, in continuing fixed increments. The overall flexibility can be increased by further stranding of the individual strands.

Figure 1-6 shows a typical cross section of a 37-strand cable. It also shows how the total circular-mil cross-sectional area of a stranded cable is determined.

Introduction to Electrical Conductors, Wiring Techniques and Schematic Reading Navy Electricity and Electronics Training Series (NEETS) - Module 4 Chapter 1: Pages 1-1 through 1-10

Introduction to Electrical Conductors, Wiring Techniques and Schematic Reading
Navy Electricity and Electronics Training Series (NEETS) - Module 4
Chapter 1: Pages 1-1 through 1-10