Reflection/Transmission Measurements Using a LadyBug PowerSensor+™

Application Note

A scalar network analyzer is a low cost easy to use solution for making reflection and transmission measurements.   This paper is devoted to the hardware required to configure a reflection/transmission test setup and methods for making quality reflection and transmission measurements, including calibration.

Reflection Measurement Solution:

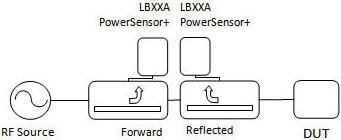
Reflection Scalar Analyzer Block Diagram

The reflection scalar network analyzer solution is used for making reflection measurements on a port of a DUT (Device Under Test).  In the solution above the RF source is connected to a Forward and Reflected signal separation device (Reflectometer).  The DUT is connected to the output of the Reflected Signal Separation Device.  The Signal Separation Devices are oriented to couple the forward and reflected signals as shown.  The coupled arms of each signal separation device are connected to an LB4XXA Power Sensor being used as the detector.

The Ladybug Technologies LB4XXA PowerSensor+ are ideal for this application because they offer:

• Easy to integrate ATE software components.
• Fast 2000 settled points/second  enabling real time measurements
• Wide -60 dBm to +20 dBm dynamic range

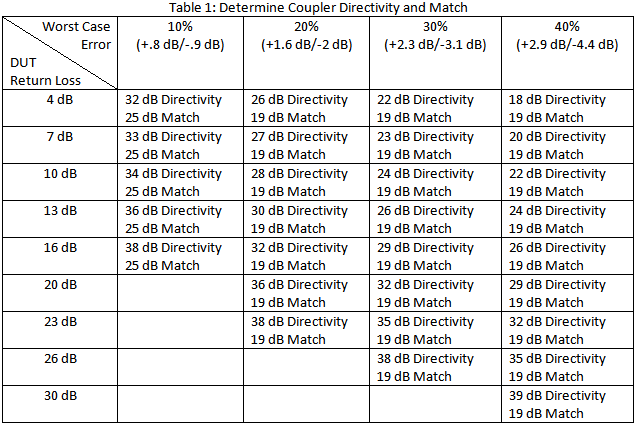
The signal separation device is often a coupler.  Consideration should be given to the coupler's directivity and match.   Usually directivity dominates measurement error.  However, as the DUT's return loss becomes smaller match becomes a more significant contributor.  Table 1 provides coupler directivity and match given a DUT's return loss and worst case error.  Worst case error assumes an open short tracking calibration has been done.

   Example 1:   Determine coupler specifications for a DUT with (expected) return loss of 15 dB and a total worst

                        case error of 40%.

   Solution 1:  Use coupler specifications for 40% and 16 dB worst case error:  Coupler directivity = 26 dB and

                      coupler match = 19 dB.  Further, maximize measurement dynamic range by selecting a coupler

                      with 10 dB coupling factor.

If avoiding calibration is desired match the forward and reflected couplers, minimizing their insertion loss.  Also minimize adaptors and cabling between the couplers and the DUT.  Unless DUT match is less than 10 dB a dual directional coupler is not recommended because of poor resulting directivity (even if the coupler has reasonably good directivity).  The tracking error is approximately twice the insertion loss of the coupler and cabling between the reflected coupler and the DUT.  Approximate worst case error is found by adding this tracking error to the error shown in the table.

   Example 2:  Determine the additional error in Example 1 if a tracking calibration is not done.

   Solution 2:  Typical insertion loss for a 10 dB coupling factor coupler is 0.5 dB.  Assume cable loss between

                      the coupler and DUT is 0.1 dB.   This additional error or tracking error is

                      1.2 dB (0.5 dB X 2 + 0.1 dB X2).

Alternatively the tracking error can be estimated (or measured by calibrating) and removed from the result.  Because tracking error is a loss, the resulting match measurement is simply offset by the estimated tracking error.  Add the tracking error to the match measurement.

   Example 3:  Assume a 17.1 dB measurement result and Example 2 configuration.  Determine the match

                      result given the tracking error offset.

   Solution 3:  15.9 dB.  Add the 1.2 dB tracking error to the 17.1 dB match measurement.

The forward signal separation device may be replaced with a two resistor power splitter, such as a Picosecond Pulse Labs 5336 or an Agilent 11667A.  The splitter offers good broadband performance however lacks in its ability to handle high power.

Maximizing Dynamic Range:

As noted in Example 1 dynamic range should be considered.  In general dynamic range is maximized by:

• Using low coupling factors.  In general default to using a 10 dB (coupling factor) coupler.
• Maximize RF source power. Keeping it within the range of the power sensors being used.  As source power begins to exceed 1/2 watt, Increase coupler coupling factor.
• Select power sensors with maximum measurement speed throughout its dynamic range.  Such as the LadyBug Technologies LB4XXA PowerSensor+ that can measure 2000 settled points per second at - 60 dBm.

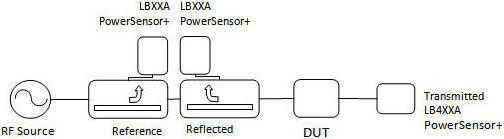
Reflection/Transmission Scalar Analyzer Block Diagram

By adding a third LBXXA Power Sensor transmission measurements (S21 or S12) can be made.  Port match of the power sensor and of the reflectometer in combination with DUT's S parameters determine errors in measuring the DUTs S21 or S12.  Measurement error for a DUT with S21 = S12 = 0 dB is typically 0.27 dB (DUT match = 15 dB, Power Sensor match = 27 dB, reflectometer match = 19 dB).  Increasing DUT S21 and S12 can reduce this error to 0.22 dB; this error would begin to rise when considerations for dynamic range are included.

Correction:

Mathematics of the correction is considered in this section.  It is assumed the user has the expertise to apply the programming examples provided in the LadyBug product literature to set up and read power measurements from the LB4XXA Power Sensor and apply those measurements to the equations below.

Reflection Measurement and Correction:

The basic measurement equations can be done in either linear or dB.  Both are presented below.  In dB form power measurements in dBm can be used directly.  In linear form the square root of linear power must be taken.

Linear form of the solution

Reflected match is

ρ = τ (b/a).

Where:

ρ is the liner reflection coefficient of the DUT;

τ is the liner tracking correction between the forward and reflected signals;

b is the linear measured reflected square root of power;

a is the linear measured forward square root of power.

All that remains is to determine the correct value of the τ.

Reflection Calibration:

The objective of the calibration is to measure τ .  τ is computed from the measurement of two calibration standards, an open and a short.  Removal of the source match error from τ is accomplished by ensuring the open and short are balanced and that their reflection coefficients are 180 degrees apart.

Measurement of the open is

ρ_O = |1| = τ_O (b_O/a_O), or

τ_O = (a_O/b_O).

Where:

ρ_O = |1|  is the liner magnitude reflection coefficient for an ideal open;

τ_O is the liner tracking measurement for the open calibration;

b_O is the linear measured reflected square root of power for the open calibration;

a_O is the linear measured forward square root of power for the open calibration.

Measurement of the short is

ρ_S = |-1| = τ_S (b_S/a_S), or

τ_S = (a_S/b_S).

Where:

ρ_S = |-1|  is the liner magnitude reflection coefficient for an ideal short;

τ_S is the liner tracking measurement for the short calibration;

b_S is the linear measured reflected square root of power for the short calibration;

a_S is the linear measured forward square root of power for the short calibration.

Determine τ by averaging τ_O and τ_S

τ = (τ_O + τ_S)/2.

It should be noted the either τ_O or τ_S may be used for τ; however the error associated with source match for the final result will increase.  This additional error may be as high as 0.4 to 0.5 dB.  If this trade off is acceptable, it would be worthwhile considering the use of 20 dB couplers and minimize the uncorrected crosstalk and avoid a calibration all together.

   Example 4:  Use 20 dB couplers in Example 2 and determine the approximate tracking.

   Solution 4:   Typical insertion loss for a 20 dB coupler is 0.12 dB.  The resulting tracking error offset would

                       be 0.44 dB (0.12 dB x 2 + 0.1 dB x 2).

Form of the solution in dB.

Return Loss is:

RL = ρ_dB = τ_dB + b_dB - a_dB.

Where:

RL = ρ_dB is the return loss of the DUT;

τ_dB is the tracking correction in dB;

b_dB is the reflected power measurement in dBm;

a_dB is the forward power measurement in dBm.

Reflection Tracking Calibration:

Measurement of the open in dB is

RL_O = ρ_dBO = τ_dBO + b_dBO - a_dBO, or

τ_dBO = a_dBO - b_dBO.

Where:

ρ_O = 0  is the return loss for an ideal open;

τ_O is the tracking measurement in dB for the open calibration;

b_O is the reflected power measurement in dBm for the open calibration;

a_O is the forward power measurement in dBm for the open calibration.

Measurement of the short in dB is

RL_S = ρ_dBS = τ_dBS + b_dBS - a_dBS, or

τ_dBS = a_dBS - b_dBS.

Where:

ρ_S = 0 is the return loss for an ideal short;

τ_S is the tracking measurement in dB for the short calibration;

b_S is the reflected power measurement in dBm for the short calibration;

a_S is the forward power measurement in dBm for the short calibration.

Determine τ by taking the linear average of τ_O and τ_S

τ = 20 x Log10( 10^(-τ_O/20) + 10^(-τ_S/20))/2.

Transmission Measurement and Correction:

Both the linear and dB form of the measurement equation is presented below.  In dB form power measurements in dBm can be used directly.  In linear from the square root of linear power must be taken before application of the equations.

Linear form of the solution

Transmission gain or loss is

L = τ_τ (c/a).

Where:

L is the liner transmission gain or loss of the DUT;

τ_τ is the linear transmission tracking correction;

c is the linear measured transmitted square root of power;

a is the linear measured forward square root of power.

Measurement of τ_τ

The objective of the calibration is to measure ττ .  ττ is measured by connecting the transmitted LB4XXX power sensor to the reflectometer; referred to as a thru.

The thru measurement is

L₁ = 1 = τ_τ (c_L/a_L), or

τ_τ = (a_L/c_L).

Where:

L₁ = 1 is the liner transmission gain for the thru;

τ_τ is the linear transmission tracking correction term;

c_L is the linear measured transmitted square root of power for the thru;

a_L is the linear measured forward square root of power for the thru.

Form of the solution in dB

Transmission gain or loss is

L_dB = τ_τdB + c_dB - a_dB.

Where:

L_dB is the dB gain or loss of the DUT;

τ_τdB is the dB transmission tracking correction;

c_dB is the dB measured transmitted power;

a_dB is the dB measured forward power.

Measurement of τ_τdB

The thru measurement is

L_1dB = 1 = τ_τdB + c_LdB - a_LdB, or

τ_τdB = a_LdB - c_LdB.

Where:

L_1dB = 0 is the dB transmission gain for the thru;

τ_τdB  is the dB transmission tracking correction term;

c_LdB is the dB measured transmitted power for the thru;

a_LdB is the dB measured forward power for the thru.

Contact Info

Orwill Hawkins

LadyBug Technologies, LLC Contact

Phone: 707-546-1050 x103

Website: www.LadyBug-Tech.com

e-Mail: Orwill@LadyBug-Tech.com

Posted  October  19, 2013