The Design of Ultra Narrow-band Amplifiers using Small Signal Varactor Up-converters for ESM, ECM, ECCM, and ELINT Applications |

The following paper titled "The Design of Ultra Narrow-band Amplifiers Using Small Signal Varactor Up-converters for ESM, ECM, ECCM, and ELINT Applications" was submitted for publication by Planar Monolithics Industries, Inc. (PMI), and has been duly accepted by the Technical Committee and Management of EWCI-2014. Dr. Alfred I. Grayzel, Dr. Ashok (Ash) K. Gorwara, Paul Kuhn Planar Monolithics Industries, Inc., Frederick, Maryland USA ABSTRACT: A method is presented in this paper for realizing tunable
amplifiers with bandwidths of less than 0.5%; without the use of superconductors and cryogenic cooling. This method
uses a small signal varactor up-converter to achieve these ultra narrow bandwidths. The equivalent circuit for the
up-converter is presented as well as the circuit configuration of the narrow band negative resistance amplifier.
The design and experimental results are presented for a 0.5% bandwidth negative resistance amplifier at 800 MHz;
using this unique circuit design. These devices and circuits can be used for electronic warfare applications such
as surveillance, electronic reconnaissance, jamming and frequency hopping. I. INTRODUCTION This paper presents a method of realizing tunable microwave amplifiers with ultra narrow bandwidths that can be less than 0.5% by the use of a varactor up-converter (UC)[1]. In the past the UC has been used to up-convert an input signal at frequency fS to a signal at frequency fS+fP where the varactor is “pumped” at frequency fP. In this paper we will use the property of the UC that when it is terminated at frequency fS in an impedance Z(ωS) where ωS=2πfS, this impedance is “imaged” at the output frequency fS+fP,[2]. For example: if a bandpass filter with a passband from 97.5 to 102.5 MHz is terminated in a negative resistance and connected to the input terminals of a UC “pumped” at a frequency of 900 MHz, then the negative resistance will be ”imaged” at the output of the UC over the frequency band from 997.5 to 1002.5 MHz. Thus the 5% bandwidth of the input circuit results in a 0.5% bandwidth at the output of the UC. If the pump frequency is tuned to 870 MHz, then the negative resistance will be “imaged” over the passband from 967.5 to 972.5 MHz. Thus by varying the pump frequency the passband can be tuned while preserving the bandwidth. The equations describing this “imaging” are presented in this paper for the small signal varactor upconverter. II. THE NEGATIVE RESISTANCE AMPLIFIER
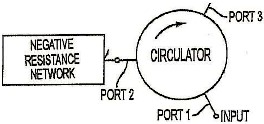
Fig.1 shows the configuration of the negative resistance amplifier described in this paper.
Fig.1 – The Negative Resistance Amplifier Configuration A circulator of characteristic impedance Z0, has port 1 as the input port, port 3 as the output port and has port 2 terminated in a tunable negative resistance network. Let us consider an idealized negative resistance network, whose input impedance has a real part equal to –R and an imaginary part equal to zero over the frequency range from f1 to f2. Outside of this frequency range the real part of the impedance is zero. Since the output power at port 3 of the circulator is equal to the magnitude squared of the reflection coefficient at port 2 of the circulator the gain of the amplifier over the frequency range from f1 to f2 is given by: G = ((1+ R) / (1- R))2 (1) Outside of this frequency range the amplifier has a gain of one. The negative resistance network shown in Fig.1 is the heart of this amplifier; it's output impedance must approximate the impedance characteristic described above over the tuning range of the amplifier. The block diagram, of the negative resistance network of Fig.1 is shown in Fig.2.
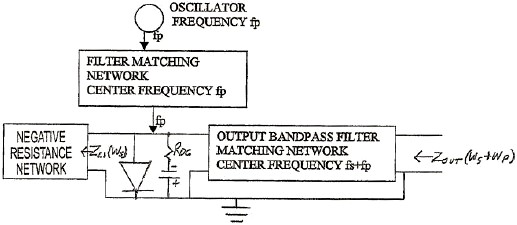
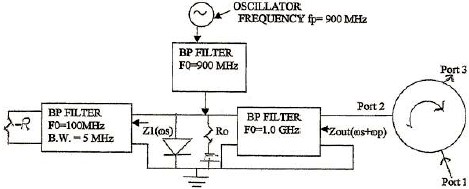
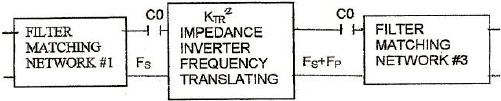
Fig.2 – The Tunable Negative Resistance Network A varactor shunted by a bias network is connected to three filter/matching networks. The first is a bandpass filter/matching network terminated in a negative resistance, which serves as the input to the up-converter. It has a passband from f1 to f2, with center frequency fS and must present a high impedance at frequencies fP and fS+fP. The second bandpass filter/matching network has a center frequency fP which is connected to a tunable oscillator tuned to fP; the pump frequency and must present a high impedance at frequencies fS and fS+fP. The third bandpass filter/matching network has a center frequency fS+fP and must present a high impedance at frequencies fS and fP. It serves as the output of the negative resistance network. Fig. 3 shows the configuration for the example cited above where fS=100 MHz, fP=900 MHz and fS+fP=1.0GHz.
Fig.3 – The Network of Fig.2 with fS=100 MHz, fP=900 MHz and fS+fP=1.0 GHz It is shown in reference [2] for the small signal UC that when the UC is terminated at its output port, in an impedance ZL2(ωS+ ωP), the input impedance of the UC is given by:
where VS is the voltage across the varactor and IS is the current flowing through the varactor at frequency fS. It is also shown that when the UC is terminated in an impedance ZL1(ωS), the output impedance of the UC is given by:
where VS+P is the varactor, IS+P is the current flowing through the varactor at frequency fS+fP., and voltage across S0 is the average susceptance of the varactor as pumped[1]. The value of (KTR)2 is given by:
where, S1 is the fundamental component of the incremental elastance pumped at frequency fP. It follows from (2) and (3) that the equivalent circuit of the UC can be drawn as shown in Fig.3, consisting of a frequency translating impedance inverter KTR with series capacitors connected to input and output. The value of these capacitors is equal to the reciprocal of the average susceptance of the varactor as pumped. The pump circuit is not shown however, (KTR)2 is a function of the current supplied by the pump oscillator at frequency fP. Thus the “imaging” referred to above is defined by (2) and (3) or by the circuit of Fig. 4. The two series capacitors can be incorporated into the input bandpass filter/matching network and the output bandpass filter/matching network.
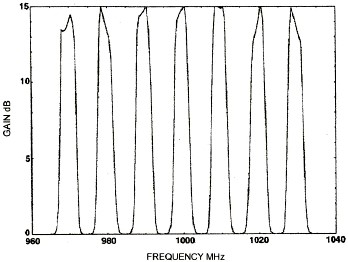
Fig.4 – The Equivalent Circuit of a Small Signal Up-Converter For example: if ZL1(ωS) has a value of -50 ohms and (KTR)2 equals 1750, then Zout equals -35 ohms, and the gain of the amplifier is found using (1) to be equal to 15 dB. Fig.5 shows a computer analysis of the gain of the amplifier shown in Fig.1 and Fig.2.
Fig.5 – Computer Generated Gain of a Negative Resistance Amplifier Tuned in 100 MHz Steps The pump frequency was tuned from 970 MHz to 1.3 GHz in 100 MHz steps. KTR was chosen at each pump frequency for a gain of 15 dB. This can be accomplished in practice by using a digitally controlled oscillator followed by a digitally controlled attenuator in the pump circuit. A six section Butterworth filter with a 5% bandwidth and a center frequency of 100 MHz was used for the input filter in this computer simulation. The output filter is a five section Tschebyscheff filter with a 0.2 dB ripple and an eight percent bandwidth. The capacitance C0 was incorporated into the first resonator of these filters. The computational procedure was as follows. ZL1(ωS) the input impedance of the input filter terminated in a negative resistance of -50 ohms was first computed. Using (3) and (4) the output impedance of the inverter was then calculated. The input impedance of the output filter terminated in Zout(ωS + ωP) was then calculated and then using eq. 1 the gain of the amplifier was computed. The computation is exact; it makes no approximations other than the assumptions of a lossless varactor and lossless filter/matching networks which have the exact response of the Butterworth and Tcebycheff filters used in the computer simulation. III. ACHEIVABLE TUNING RANGE If fS equals 100 MHz and fP is tuned over the frequency band from 850 to 950 MHz, then the output frequency of the UC will vary from 950 to 1050 MHz. The output filter/matching network must have a passband from 950 to 1050 MHz in order to pass these frequencies and therefore, cannot reject the pump frequency when the pump is tuned to 950 MHz. Thus the pump tuning range must be smaller than 850 to 950 MHz and the output tuning range must be smaller than 950 to 1050 MHz. Thus for a ratio of the output to the input frequency of 10, the percent tuning range of the output frequency is less than 10%. Let us consider the case where fS is equal to 100 MHz and fP is tuned over the frequency band from 250 to 350 MHz. The output of the up-converter will then vary from 350 to 450 MHz. The output filter/matching network must then have a passband from 350 to 450 MHz and therefore cannot reject the pump frequency when the pump is tuned to 350 MHz. Thus the pump tuning range must be smaller than 250 to 350 MHz and the output tuning range smaller than 350 to 450 MHz. Thus for a ratio of the output to the input frequency of 4, the output frequency percent tuning range is less than 25%, and a 5% input bandwidth yields an output bandwidth of 1.25%. There is thus a tradeoff between narrow bandwidth and tuning range.
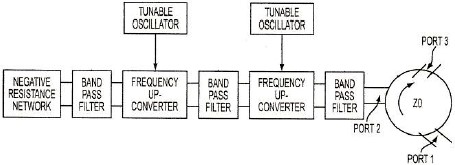
To achieve greater tuning ranges the circuit of Fig.6 can be used, where two UCs are cascaded.
Fig.6 – A Negative Resistance Amplifier Configuration with Two Cascaded Frequency Up-Converters If the first UC, has an input frequency of 100 MHz and has a pump frequency that can be tuned from 250 to 325 MHz then the output frequency of this UC can be tuned from 350 to 425 MHz. If the second UC has an input bandwidth from 350 to 425 MHz and has a pump frequency that can be tuned from 450 to 775 MHz then the output frequency can then be tuned using digitally controlled oscillators, from 800 to 1,200 MHz. Thus for a ratio of output to input frequency of 10, the percent tuning range of the output frequency for this configuration is 40%. To achieve even narrower bandwidths the configuration of Fig. 7 can be used.
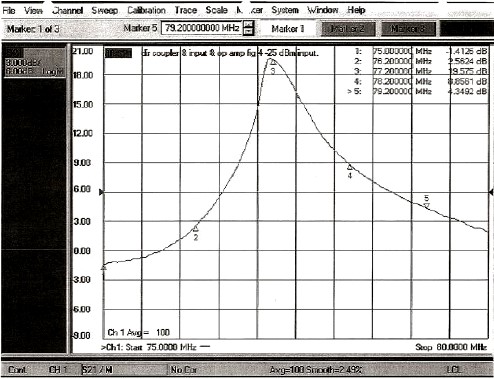
Fig.7 – Two Cascaded Frequency Up-Converters Configured to Achieve Narrower Bandwidth If as shown in Fig. 7 a 100 MHz signal is up-converted to 1 GHz in the first up-converter and to 10 GHz in the second up-converter a 5% bandwidth at the input frequency of 100 MHz results in a 0.05% bandwidth at the output frequency of 10 GHz. IV. EXPERIMENTAL RESULTS An op-amp followed by a bandpass filter with a 5% bandwidth was used for the negative resistance network shown in Fig.2. The gain of this circuit as an 80 MHz negative resistance amplifier is shown in Fig.8
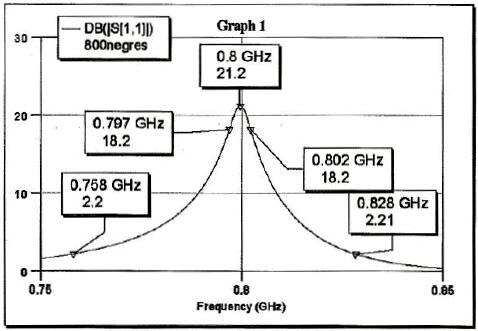
Fig.8 – A Negative Resistance Amplifier at 80 MHz The maximum gain was set at 19.6 dB and the gain fell by 14 dB in a bandwidth of about 4.5%. The negative resistance presented by this negative resistance circuit is then up-converted to 800 MHz. Fig.9 shows the computed gain of the amplifier at 800 MHz. Measured data will be presented at the conference.
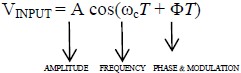
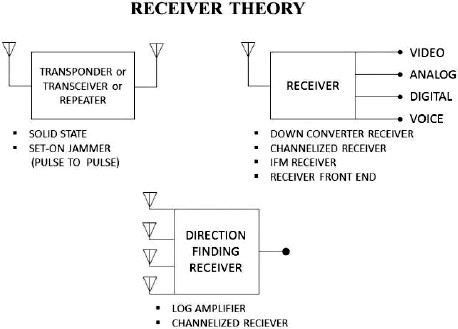
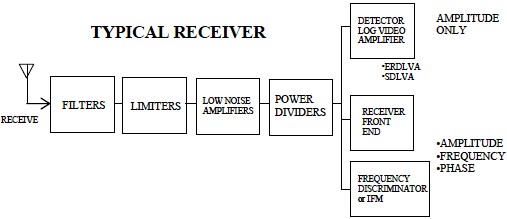
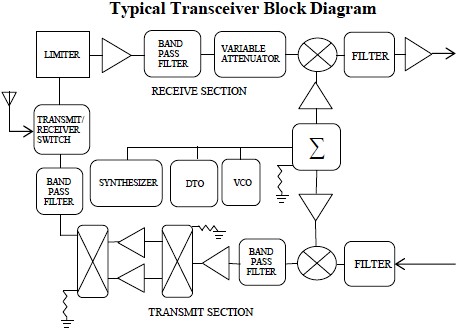
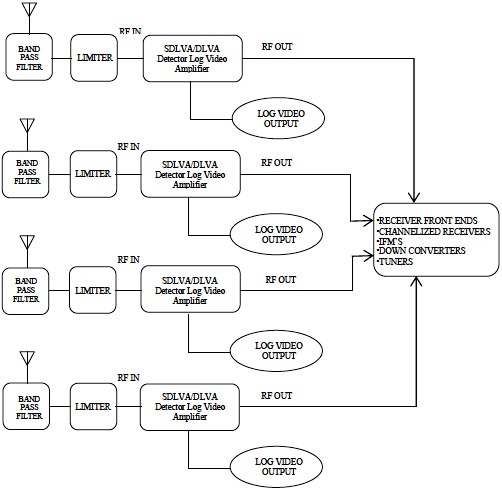
Fig.9 – Computed Gain of Amplifier at 800 MHz V. ELECTRONIC WAREFARE APPLICATIONS The research & development work being reported in this article is basically to report on how it is possible & achievable to increase the Dynamic Range & Sensitivity of RF/Microwave Receivers used in Electronic Warfare Applications by basically controlling & narrowing the bandwidth of a Receiver. The issue of bandwidth for ECM Receivers was earlier researched and reported by the author in a reference paper [3] as that time there were no easy solutions to narrowing the bandwidth, which are now possible with the advent of the ultra narrow band amplifiers being reported in this paper that could lead to simply the design of ECM Receivers not having to deal with the image signals but to concentrate on the information of the modulated signals that are present on the real carrier. The Receivers maybe superheterodyne types single or multiple, Down & Upconverters, Converters, Up/Down converters, Channelized, Tuners, Instantaneous Frequency Monitors(IFM's), Detector Log Video Amplifiers,(DLVA's), Successive Log Video Amplifiers (SDLVA's), Transponders or Transceivers, Direction Finding(DF), or Radar Warning(RWR) or used in set on Jammers. To understand & apply these Ultra Narrow Band Amplifiers reported here, for ESM, ECM, ECCM, and ELINT applications one must review the theoretical equations that govern any Receiver design which are as follows: Minimum Detectable Signal (MDS): In Reference [4] more details are given on the theoretical equations and derivations for Diode Detector Receivers and Mixer or Down Converter Type receivers. The lowest level signal that is detectable by the Receiver that can be calculated to the first order is by the equation, MDS= -114 + NF + 10 log (Br) NF is in dB Br = RF channel bandwidth (MHz) If detection video bandwidth is known, the equation becomes: MDS= -114 + NF + 10 log sqrt(2BrBv – 2Bv2) Bv = video detection bandwidth (MHz) Tangential Sensitivity (TSS): [5] In this reference Theory of DLVA, ERDLVA and SDLVA designs is given and explained. MDS + 4 dB Minimum Operating Sensitivity: [6] In this reference Glossary of Terms and Definition is given and explained TSS + 5 dB VI. CONCLUSION From the above equations one can view that the Sensitivity and Dynamic range of a Receiver can be increased by reducing the bandwidth of the Receiver Amplifiers. Lower the bandwidth higher is the Sensitivity. Almost all Electronic Warfare Receivers and Systems are basically trying to solve the unknown equation below and determine what all the parameters are in the equation,
The topology or block diagrams of various Receiver types used in Electronic Warfare applications are shown below as:
VII. REFERENCES [1] P. P. Penfield, and R. P. Rafuse, VARACTOR APPLICATIONS, Cambridge Mass. The M.I.T. Press 1962 [2] A. I. Grayzel, VERY NARROW-BAND TUNABLE FILTERS AND AMPLIFIERS USING A SMALL SIGNAL VARACTOR UP-CONVERTER, 2012 IEEE International Conference on Wireless Information Technology and Systems (ICWITS) [3] A. K. Gorwara, "PHASE AND AMPLITUDE BALANCE, KEY TO IMAGE REJECT MIXERS", Microwaves, October 1972. https://www.pmi-rf.com/plamic/finalreports/pabalance.pdf [4] Equation 1V-2,Page 1V-10, "DIODE BEACON TECHNIQUES” by Dr Ashok Gorwara for Rome Air Development Center, Griffis Airforce Base, Rome New York, 13440. Stanford Research Institute(SRI) Project 1970,Contract No F30602-72-C-0444, January 1974. https://www.pmi-rf.com/plamic/finalreports/diode.pdf [5] DLVA'S SOLID STATE RECEIVER COMPONENTS - Application Note-Theoretical Background - Log Amplifier Design by Planar Monolithics Technical team(PMI), Frederick, MD, USA- Jan 26 2008, https://www.pmi-rf.com/Products/dlva/ApplicationNotes-DLVA.htm [6] DEFINITIONS AND A GLOSSARY OF TERMS FOR DETECTOR LOGARITHMIC VIDEO AMPLIFIERS AND RELATED PRODUCTS by Planar Monolithics technical team(PMI), Frederick, MD, USA, August 15, 2008, https://www.pmi-rf.com/Products/dlva/DLVA-GlossaryofTerms.htm BIO DATA OF AUTHOR(S)
Posted January 14, 2014
|
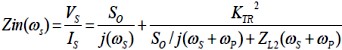 (2)
(2) 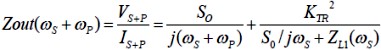 (3)
(3) 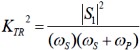 (4)
(4) 
 Alfred
I. Grayzel (M'55- SM'85- LM '92) was born in Brooklyn N.Y. in May 24, 1933. He received a B.A. from Columbia College
in N.Y.C. in 1954 and a B.S.E.E. from the Columbia School of engineering in 1955. He received an M.S.E.E. and a
Ph.D. in electrical engineering from M.I.T. in 1961 and 1963. He spent 17 years of his career at M.I.T.'s Lincoln
Laboratory as a staff member. In 1975 he founded A.I. Grayzel Inc. which manufactured unconditionally stable varactor
frequency multipliers and up-converters. The company was acquired by the Anzac Corporation in 1985. He is currently
a consultant to PMI, USA.
Alfred
I. Grayzel (M'55- SM'85- LM '92) was born in Brooklyn N.Y. in May 24, 1933. He received a B.A. from Columbia College
in N.Y.C. in 1954 and a B.S.E.E. from the Columbia School of engineering in 1955. He received an M.S.E.E. and a
Ph.D. in electrical engineering from M.I.T. in 1961 and 1963. He spent 17 years of his career at M.I.T.'s Lincoln
Laboratory as a staff member. In 1975 he founded A.I. Grayzel Inc. which manufactured unconditionally stable varactor
frequency multipliers and up-converters. The company was acquired by the Anzac Corporation in 1985. He is currently
a consultant to PMI, USA.  Dr.
Ashok(Ash) Gorwara attended University of London for BSEE, MSEE, Ph.D/DSEE doctoral studies. Post-doctoral, Lecturer
at MIT, & Northeastern University, Boston, USA going onto further Research/Development at MIT-Lincoln Laboratories &
Stanford Research (SRI), California for Electronic Warfare Components, Subsystems & Satellite Communications.
Presently President & CEO, Owner, Chief Technical Officer of PMI, USA
Dr.
Ashok(Ash) Gorwara attended University of London for BSEE, MSEE, Ph.D/DSEE doctoral studies. Post-doctoral, Lecturer
at MIT, & Northeastern University, Boston, USA going onto further Research/Development at MIT-Lincoln Laboratories &
Stanford Research (SRI), California for Electronic Warfare Components, Subsystems & Satellite Communications.
Presently President & CEO, Owner, Chief Technical Officer of PMI, USA