Here is the "Electricity - Basic Navy Training Courses"
(NAVPERS 10622) in its entirety. It should provide one of the Internet's
best resources for people seeking a basic electricity course - complete with examples
worked out. See
copyright. See
Table of
Contents. • U.S. Government Printing Office; 1945 - 618779

Chapter 7
ELECTRICAL POWER
FORCE
Scientists and technicians make a point of specifically defining all the
terms they use. They like their language to say exactly what they mean. This is
necessary because scientists use technical terms in explaining their work. With
a good working knowledge of such terms as force, power, work, EMF, current, and
resistance, you'll be far more savvy about your own work. Too, you'll want to be
sure so that you can shoot the breeze about your job. Knowing exactly What certain
words MEAN helps a lot!
You often HEAR the word FORCE. But you USE force far. more) often than you hear
the word. Every time you lift something, you use force. Every time you move, you
have exerted force. A ship moves through the water because of force. In fact, every
time anything moves or tends to move, force has been exerted. Force may be a push
or a pull. FORCE then, IS THAT WHICH PRODUCES MOTION OR TENDS TO PRODUCE MOTION.
Consider the force of GRAVITY. It causes bodies to move toward the earth. Suppose
you put a box on a table. The box tends to move DoWNWARD because of gravity but
the table exerts an UPWARD force - the two forces are balanced. However, if the
box is "too heavy" for the table, the table cannot exert enough upward
force to balance the pull of gravity and the table collapses.
The force exerted by a propeller is a MECHANICAL force. The explosion of hydrogen
and oxygen to form water is a CHEMICAL force. The force which causes electrons to
flow is an ELECTROMOTIVE force and its unit is the VOLT. There are many kinds of
force, but they ALL produce or tend to produce motion.
WORK
WORK IS A FORCE ACTING THROUGH SPACE. Imagine that you push with. all your strength
against a steel bulkhead. You probably think you've <;lone, work but technically
you HAVEN'T. True, you have exerted force on the bulkhead, but since the bulkhead
hasn't moved, NO WORK has been done. Now imagine that you exert the same force lifting
a 200-pound shell from the deck to a shelf 4 feet high. WORK HAS BEEN DoNE, because
the force acted through space'. You exerted a 200pound FORCE through a DISTANCE
of 4 feet.
Work = force x distance
so in this case -
Work =200 pounds x 4 feet = 800 foot-pounds (ft.-lb.)
notE that work and force are different. Force is exerted whenever a body
is pushed or pulled BUT work is done only IF the BODY MOVES. In electricity, the
unit of work is the JOULE.
ELECTRICAL WORK = VOLTAGE x COULOMBS = JOULES
The JOULE, by itself, has relatively little use because it does not take
into consideration the factor of TIME. That is, it might take 2 seconds or 2 days
for 120 volts to move 1 coulomb (6.3 billion billions electrons); and in either
case, you would have done 120 x 1 = 120 joules of electrical work. So time is really
important - and that brings you to power.
POWER
POWER IS the TIME RATE OF DoING WORK. This relation is expressed -
Power = Work/Time
You have learned that the amount of WORK done has nothing to do with the time
it takes to do the work. BUT the amount of POWER depends on HOW FAST that work can
be done. You know that a steam shovel has a great deal more POWER than a man. Both
can do the same amount of work but the steam shovel will do it a lot FASTER. For
example, say that 1,000 pounds of earth must be raised 20 feet. The work is -
Work = force x distance = 1,000 x 20 = 20,000 foot-pounds.
The steam shovel does the job in one scoop, taking 2 seconds. The man does
the job in 20 minutes (or 1,200 seconds). The steam shovel has -
Power = Work/Time = 20,000/2 = 10,000 ft-lb. per second
of power
The man has -
Power = Work/Time = 20,000/1,200 = 16.7 ft-lb. per
second of power
The steam shovel has exerted approximately 600 times as much POWER as the
man even though the WORK done by both is equal.
The mechanical unit of power - FOOT-POUNDS PER SECOND - is too small for practical
use. In the early days, power was generally supplied by horses, and experiments
indicated that an average horse could do 550 foot-pounds of work per second. This
led to the establishment of a larger unit-the HORSEPOWER (hp).
HP = 550 FT.-LBS. PER SECOND
What was the HP of the steam shovel in the preceding example?
10,000 ft.lbs. per sec./550 ft.lbs. per second = 18.2
hp
What was the HP of the man?
16.7 ft.-lbs. per second/550 ft.-lbs. per second -
0.032 hp
Power in the electrical system is measured in WATTS.
Power = Work/Time = Volts x Coulombs/Time = Watts
(w.)
Do you recognize the expression - Coulombs/Time? In Chapter 3, you learned
that coulombs divided by time was the time rate of flow of current - the AMPERE.
So you can substitute AMPERE for Coulomb/Time in the above equation, and the equation
becomes -
Power = volts X amperes = Watts, or -
P=E x I
POWER IS AN IMPORTANT MEASURE IN ELECTRICITY. It tells you how much you
can expect from a motor or generator.
Study the circuit in figure 34. It shows a motor connected to its generator;
and meters are installed to read the values of current and voltage in the circuit.
By multiplying the ammeter and volt-meter readings, you get the power consumed by
the motor -
P = E x I = 120 x 8 = 960 watts
which means that this motor CONSUMES 960 watts of power.
By measuring the amount of mechanical work a number of electric motors did in
one second, it was determined that- 746 Watts = 1 hp

Figure 34. - Power consumption of a motor.
Does the motor DELIVER 960 watts, or 960/746 = 1.29 hp, of power? No, because
some of the power is lost within the motor. This loss is caused by internal heat
and friction. All machines lose some power by heat and friction. If they didn't,
they would be 100 percent EFFICIENT and there would be perpetual motion. EFFICIENCY
is the percentage of the total input power that is actually delivered as output.
Motors deliver their power at their shafts. Say that this particular motor is a
one-hp job. This means that the motor DELIVERS one hp AT ITS SHAFT.
What is its efficiency?
INPUT = 960 watts
OUTPUT = 1 hp = 746 watts
EFFICIENCY = Output/Input
= 746/960 = 0.777, or 77.7%
The motor is 77.7 percent efficient - in other words, it delivers 77.7 percent
of the power it consumes. The balance of power - 22.3 percent is lost as heat and
friction. Look at figure 35. It shows the power and the power losses as a picture.
If you follow the arrows through this picture of a motor, you will find the input
power is ELECTRICAL POWER. It splits up in the motor, going in two directions. The
losses in the form of heat are radiated upward, and the output in the form of MECHANICAL
POWER is delivered by a rotating shaft. This gives you the definition of a motor
- A MACHINE WHICH CONVERTS ELECTRICAL ENERGY INTO MECHANICAL ENERGY. (Just the opposite
to the action of a generator.)
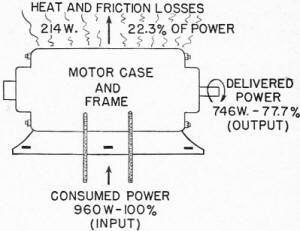
Figure 35. - Delivered and lost power in a motor.
How much work is this motor capable of doing? Since 1 hp = 550 ft-lbs. per
second, the motor can exert a force of 550 pounds through 1 foot of space every
second. Or, 275 pounds through 2 feet of space every second. Or, 55 pounds through
10 feet of space every second. You'll notice that the force decreases as the speed
increases.
To be sure you understand these terms, consider a harder example. Figure 36
shows a circuit involving a 10 hp motor, a generator, meters, and a 'l,000-foot
length of double wire connecting lines.

Figure 36. - Power loss in a long line.
The generator furnishes 440 volts of EMF, but the motor draws 25 amperes
at only 390 volts. The difference -50 volts - is used in pushing the current through
the 2,000 feet (1,000 ft. for each wire) of connecting wire.
You can calculate the resistance of this wire -
R = E/I = 50/25 = 2 Ω
which means that 50 volts of force are used in pushing 25 amperes of current
through 2,000 feet of wire having 2 ohms of resistance.
How much power is consumed by the motor?
P = E x I = 390 x 25 = 9,750 w
What is the efficiency of this 10 hp motor?
Efficiency = output/input = 10 x 746/9.750 = 7.460/9,750
= 76.5%
How much power is lost in the motor by heat and friction?
Losses = input - output = 9,750 - 7,460 = 2,290 w.
What is the power consumed by the line in delivering current to the motor?
P = E x I = 50 x 25 = 1,250 w.
As a check, you know that total power furnished, minus all losses, should give
the power output of the motor. In this case, 440 x 25 = 11,000 watts is the power
furnished. The losses are 2,290 + 1,250 = 3,540 watts. The output then is 11,000
- 3,540 = 7,460 watts. This checks with the rated output.
Remember - whenever work must be done, power is consumed doing it. It requires
work to force current through a wire - in this case, 1,250 watts of power is consumed
by the wire. It requires work to overcome the friction of the motor and force current
through its windings - 2,290 watts of power is consumed in doing this work. Finally,
the motor is capable of furnishing 10 hp or 7,460 watts at its shaft to do work.
The power equation may be used in three forms depending on the problems to be
worked -
P = EI; E = P/I; I = P/E
EXAMPLES
1. Determine the value of current in a 100 watt lamp on a 115 volt line.
I = P/E = 100/115 = 0.87 amp.
2. Determine the potential drop of a line which consumes 1,200 watts in carrying
60 amperes.
E = P/I = 1,200/60 = 20 v.
3. Determine the power consumed by a 440 volt motor, if it draws 22 amperes.
P = E x I = 440 x 22 = 9,680 w.
4. What is the hp of the motor in question 3?
hp = P/746 = 9,680/746 = 13 hp
LARGE AND SMALL UNITS
You ordinarily would measure butter by the pound and coal by the ton. Think
how clumsy it would be to reverse this procedure - butter by the ton and coal by
the pound. The simple units of electrical measure - volts, amperes, ohms, and watts
- prove to be clumsy when very LARGE or extremely SMALL quantities are involved.
A system of pre-fixes has developed for use in measuring large and small quantities
of electrical units. The table below gives the common prefixes used in electricity.
Each prefix can be used with any of the electrical units. For example, instead of
saying "a 10,000 watt generator," it is handier to say "a 10 KILOWATT
generator." Instead of writing "0.010 amperes" it is easier to write "10
MILLIAMPERES." In testing insulation you will use MEGOHMS instead of millions
of ohms. In radio work, the MICRO- and MILLI- prefixes are constantly used.
MEGA ................ MILLION (1,000,000)
KILO ................. THOUSAND (1,000)
1 MILLI
.............. ONE-THOUSANDTH (1/1,000)
1 MICRO
............ ONE-MILLIONTH (1/1,000,000)
Chapter 7 Quiz
(click here)
|



