Drawing a Circle with a Framing Square and 2 Nails |
|
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 "Squaring the circle" may as yet be an unattainable goal for even the best mathematicians, but the November 2012 edition of The Family Handyman magazine had a tip for how to use a square (of the framing type) and two nails to draw a circle. The author comments, "Don't ask us why this process works; all we know is that it does." Out of curiosity, I dug out my father's old Audels Carpenters and Builders Guide (printed in 1945) to see if it described the method and if it did, was there an explanation offered. It did, and he did. Read on... Make a circle with a square "Here's a tip for laying out small circles or parts of circles. Tack two nails to set the diameter you want, then rotate a framing square against the nails while you hold a pencil in the corner of the square. You might need to rub a little wax or some other lubricant on the bottom of the square so it slides easily. Don't ask us why this process works; all we know is that it does."
The Pythagorean theorem is the key, of course, for explaining the reason. For any right triangle:
where 'a' and 'b' are the lengths of the two perpendicular sides, and 'c' is the length of the hypotenuse. The same equation also happens to be (not by coincidence) the equation for a circle of radius 'c,' with the center at point (0,0). So, it stands to reason that if all of the parameters are met (three intersecting straight sides with a right angle between two of them), then the locus of points of all permissible value pairs (a,b) will result in a circle. It does not matter whether your value of 'c' represents a radius or a diameter. The hypotenuse will always be the length between the two nails and sides 'a' and 'b' will always be the distance between each nail and the 90° vertex. QED
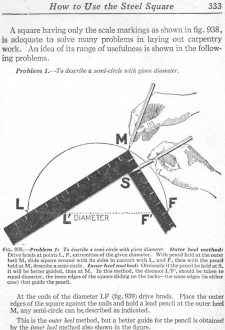
Here is what is included in the manual: Outer heel method: Drive brads at points L, F, extremities of the given diameter. With pencil held at the outer heel M, slide square around with its sides in contact with L, and F, then with the pencil held at M, describe a semi-circle. Inner heel method: Obviously if the pencil be held at S, it will be better guided, than at M. In this method, the distance L'F' should be taken to equal diameter, the inner edges of the square sliding on the tacks-the same edges (in either case) that guide the pencil.
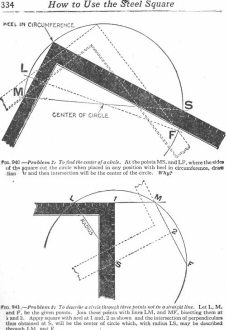
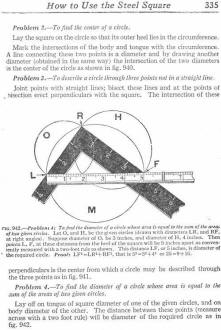
This is the outer heel method. but a better guide for the pencil is obtained by the inner heel method also shown in the figure. FIG. 940 - Problem 2: To find the center of a circle. At the points MS, and LF, where the sides of the square cut the circle when placed in any position with heel in circumference, draw diameter and then intersection will be the center of the circle. Why? FIG. 941 - Problem 3: To describe a circle through three points not in a straight line. Let L, M, and F, be the given points. Join these points with lines LM, and MF, bisecting them at 1 and 2. Apply square with heel at 1 and 2 as shown and the intersection of perpendiculars thus obtained at S, will be the center of circle which, with radius LS, may be described through LM and F. To find the center of a circle. Lay the square on the circle so that its outer heel lies in the circumference. Mark the intersections of the body and tongue with the circumference. A line connecting these two points is a diameter and by drawing another diameter (obtained in the same way) the intersection of the two diameters is the center of the circle as shown in fig. 940. To describe a circle through three points not in a straight line.
To find the diameter of a circle whose area is equal to the sum of the areas of two given circles. Let O, and H, be the given circles (drawn with diameters LR, and RF at right angles). Suppose diameter of O, be 3 inches, and diameter of H, 4 inches. Then points L, F, at these distances from the heel of the square will be 5 inches apart as conveniently measured with a two-foot rule as shown. This distance LF, or 5 inches, is diameter of the required circle. Proof: LF2 = LR2 + RF2, that is 52 = 32 + 42 or 25 = 9+16. (this is as close as they come to explaining the phenomenon, but not really).
Posted September 1, 2021 |
 "
" They're either very honest or they don't think
the average reader would understand the explanation.
They're either very honest or they don't think
the average reader would understand the explanation. 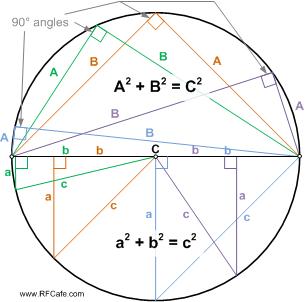 a2 + b2 = c2,
a2 + b2 = c2,